Shading (Illumination, Shading, Graphics Pipeline)

到目前为止我们已经介绍：MVP & Viewport Transformation、Rasterization

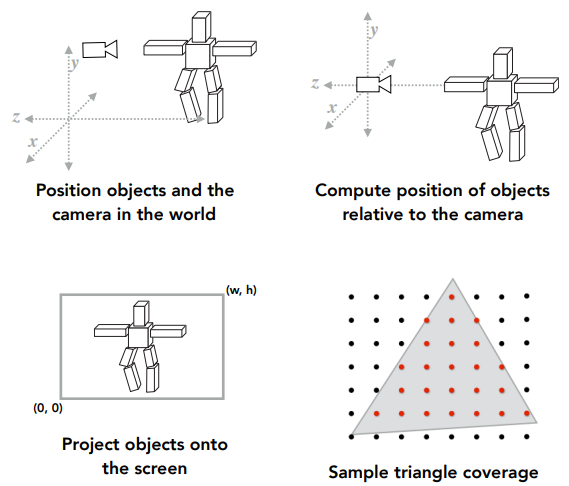
1. 在世界中定位物体和相机
2. 计算物体相对于相机的位置
3. 将对象投影到屏幕上
4. 三角形覆盖范围示例
   

我们现在还缺少 着色 Shading。

着色 Shading

着色的定义，在这门课中：对不同的物体，应用不同的材质。

一个简单的着色模型（Blinn-Phong 反射模型）

镜面高光 Specular highlights、漫反射 Diffuse reflection、环境光 Ambient lighting

着色是局部的，计算在一个特定着色点反射到相机的光。

考虑任何一个点的着色情况，就只看该点和它对应的下面几个方向，而不考虑其他物体的存在（可能有光线遮挡）

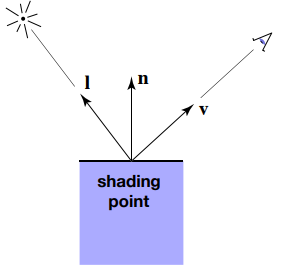
Inputs:

• 观测方向 Viewer direction, $\widehat v$
• 表面法线 Surface normal, $\widehat n$
• 光照方向 Light direction, $\widehat l$(for each of many lights)
• 表面参数 Surface parameters (color, shininess, …)
  

这并不会产生阴影 shadow，shading ≠ shadow。

因为着色有局部性，在本该有阴影的着色点上，我们没有考虑其他物体对光线的遮挡，所以着色可以看到明暗变化，但是不会产生阴影，阴影的生成在之后再说

漫反射 Diffuse Reflection

一个光线照射到某一点后，会被均匀的散射到各个方向上，这就叫漫反射。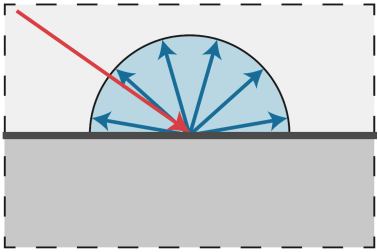

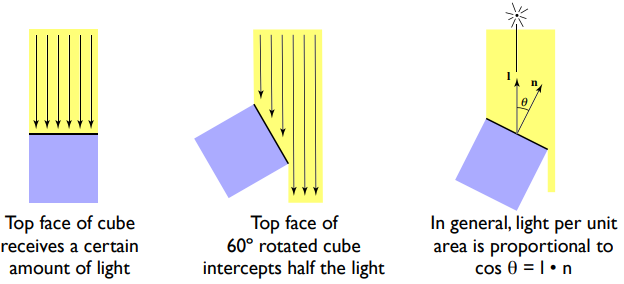
但接收到多少光 light（能量 energy）呢？Lambert余弦定律

• 立方体的顶面接收一定量的光
• 60° 旋转立方体的顶面拦截一半的光
• 一般来说，单位面积的光量与 $\cos\theta = \widehat l \cdot\widehat n$成正比
  

光衰减 Light Falloff

从一个点光源在某一时刻向外发出的能量，以一个球壳来表示，球壳随时间变大（面积 $S=4\mathrm{πr}^2$），而由能量守恒定理，可得：某一点可接收到的光量与光线传播的距离成平方反比（定义单位距离下为 I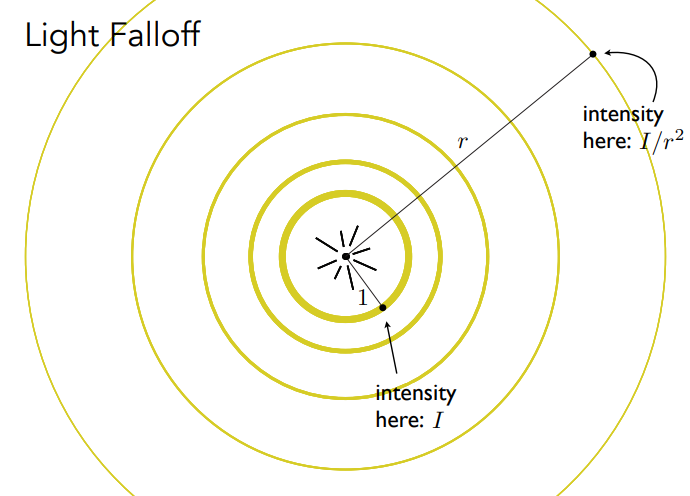

Lambertian (Diffuse) Shading

漫反射的结果与观测方向 $\widehat v$无关，对某一点，从不同位置看向它，都是一样的。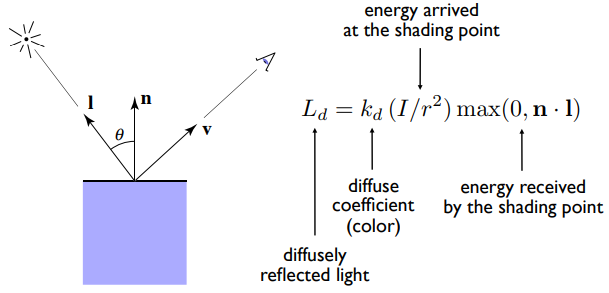

$\cos\theta = \widehat l \cdot\widehat n$即Lambert余弦定律，而结果为负时，光照方向与法线方向夹角为钝角，我们认为对反射来说没有什么物理意义，所以取 $max(0, \widehat l \cdot\widehat n)$

对某个点来说，这个点为什么会有颜色？

这个点会吸收部分的能量，将不吸收的能量反射出去，任何不同的点，有不同的吸收率，就会产生不同的颜色。
定义漫反射系数kd，kd = 1 表示该点完全不吸收能量（接收多少反射多少，白色），kd = 0 表示完全吸收（所有能量都被吸收了，没有能量被反射出去，黑色），所以 kd 表示了一个明暗，或者这个点本身吸收了多少能量。
如果我们把 kd 表示成一个三维向量，分别表示RGB三通道的值（0~1），那么就定义了在当前的 shading point 上的一个颜色。

Ld 是漫反射后辐射的总能量，均匀散射后的某一个光线是不是应该再乘上一个系数？
关于漫反射系数 kd，这里的模型并不准确，是一个经验模型，并不是完全符合物理的模型，不太考虑物理真实性，后面光线追踪还会说。

漫反射可以看作一个 shading point 吸收光后变成一个新的光源，向外辐射能量。

镜面反射（高光） Specular Term (Blinn-Phong)

高光，比较光滑的物体，反射方向都比较接近镜面反射（比如镜子，无限光滑），什么时候能看到高光？按照经验也就是观测方向和镜面反射方向接近的时候。

镜面反射的强度取决于观测方向，观测方向 $\widehat v$与镜面放射方向 $\widehat R$越接近，镜面反射效果越亮。（Phong 高光：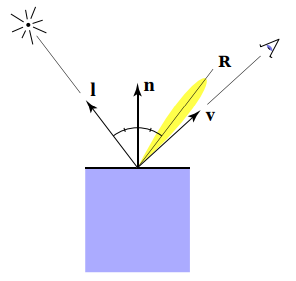

观测方向 $\widehat v$与镜面反射方向接近 ⇔ 半程向量 $\widehat h$与法线方向 $\widehat n$接近，通过向量点乘来衡量“接近”（向量夹角）（Blinn-Phong 高光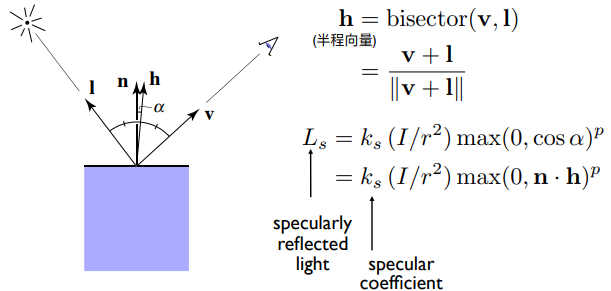

判断观测方向 $\widehat v$与镜面放射方向 $\widehat R$是否接近，称作 Phong 反射模型；判断半程向量 $\widehat h$与法线方向 $\widehat n$是否接近，称作 Blinn-Phong 反射模型。反射方向不太好算，而半程向量向量计算方便，$normalize(\widehat v+\widehat l)$，减少了计算量。

$k_s$ 和漫反射中的 $k_d$ 类似，但是对高光项，通常我们认为是一个白色的，大概可以理解为亮度值。

我们可以看出，这个公式只考虑了有多少能量到达这个 shading point，而没有考虑有多少能量被吸收了。实际上是需要考虑的，但是这里没有考虑是因为 Blinn-Phong 模型做了简化，是一个经验性处理，并不完全符合物理模型。

我们用向量点乘 $\widehat n\cdot\widehat h$衡量两个向量是否接近，与漫反射公式分析同理，所以有 $max(0, \widehat n\cdot\widehat h)$，但是为什么还要一个指数 p 次幂？

向量之间夹角余弦确实能体现两个方向之间是否接近，但是我们会发现 $cos\alpha$ 的容忍度太高了（衰减太慢），比如这两个方向夹角 45° 时，我们觉得已经离的挺远了，不应该看到明显的高光，但是 cos45° 仍然是一个相对较大的值，也就是说只用 $cos\alpha$ 不能比较合理的生成我们想要的高光。

我们平常认为高光是非常量并集中在一个很小的区域，这也说明这两个方向只要离开的稍微远一点，就不应该能看到高光了，离的非常近才认为能看到高光。所以我们加了一个指数，可以看到随着指数的增加（加快角度增大时的衰减速度），就更近似的表达我们想要的方向夹角与生成高光强度之间的关系。

正常情况下，在 Blinn-Phong 模型里，这个 p 值 大家会用 100~200，下图中到 64 幂次是不太够的。总的来说，p 是用来控制高光的大小或者集中程度。（其实相当于物体的光泽度，跟物体材质有关

余弦幂图，增加余弦的幂次 p 可以缩小反射波瓣。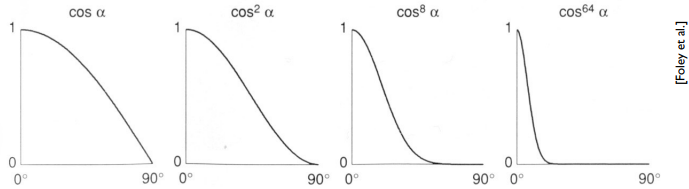

下图展示了镜面反射系数 $k_s$ 和余弦幂次 $p$ 对镜面反射高光结果的影响。

为了方便观察，这里显示的是漫反射项和高光项加在一起的结果，因为高光项太小了，如果单独看高光的话，看到的就只是一个点（或一片白色）。

环境光 Ambient Term

环境光是模拟光线经过多次反射、折射等消耗能量后入射到摄像机的光。

物体的某些地方不可能直接被光源照亮，但是也不是完全暗的，因为有很多光线被弹射很多次，从四面八方打到任何一个其他的点上，所以环境光是一个很复杂的东西。

我们做一个大胆的假设，认为任何一个点接收到来自环境的光永远都是相同的，而这个强度叫做 $I_a$，同样任何一个点当然可以有自己的颜色，所以也定义一个环境光系数 $k_a$，于是我们得到了一个近似的环境光 $L_a=k_aI_a$。

环境光是不依赖于任何东西的着色，跟光照方向 $\widehat l$和观测方向 $\widehat v$等无关，也就是一个常数（其实就是某一种颜色，保证没有地方是完全是黑的），我们添加恒定颜色以考虑忽略的照明并填充黑色阴影，这是根据经验来做的一个近似效果。（这里只是一个大胆的假设，实际上如果要非常精确的计算环境光，需要全局光照的知识。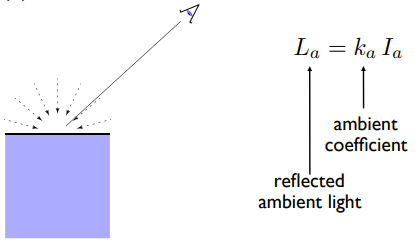

Blinn-Phong 反射模型

把所有的项加起来，就是 Blinn-Phong 反射模型。

着色频率 Shading Frequencies

下图三个球拥有完全相同的几何形状（从球的边界可以看出来，其实用的是一个模型）。为什么着色之后结果各不相同？就是着色频率的差异。

对每个三角形进行着色 Shade each triangle (flat shading)

• 每个三角形是一个平面：三角形的两边做一个叉积，求出这个三角形的法线
• 三角形内部不会有着色的变化，结果不是很好
  

对每个顶点进行着色 Shade each vertex (Gouraud shading)

• 对任意一个顶点，求出它的法线
• 逐顶点做着色，三角形内部的颜色通过差值的方法算出来
• 对三角形比较大的情况（模型不够精细），高光不明显
  

对每个像素进行着色 Shade each pixel (Phong shading)

• 对三角形内部每一个像素差值得到法线方向
• 计算每个像素的着色
• Blinn-Phong 反射模型是一个着色模型，这里 Phong shading 是一个着色频率
  

Shading Frequency: Face, Vertex or Pixel

三种着色频率的区别也取决于具体的模型。

如下图，当模型非常精细，顶点数很多的时候，Flat Shading 的结果与 Phong Shading 的结果也相差无几。效率上模型太复杂也可能三角形数比像素数还多，此时 Phong Shading 效率反而比 Flat Shading 要高。

定义逐顶点的法线

理想情况下，我们知道这个模型的形状，比如用一堆三角形表示一个球，那就可以根据球心位置和顶点位置做一个向量即为顶点的法线向量，但实际上，我们并不能知道具体表示的原型是什么，所以我们做一个近似。

对每个顶点，它是周围三角面片的公共顶点，那么这个顶点的法线，就认为是相邻的这些面的法线的平均。当然可能有的三角面片非常小，有的非常大，那么大的三角形应该会贡献的更多，所以根据面积做一个加权平均会得到更好的结果。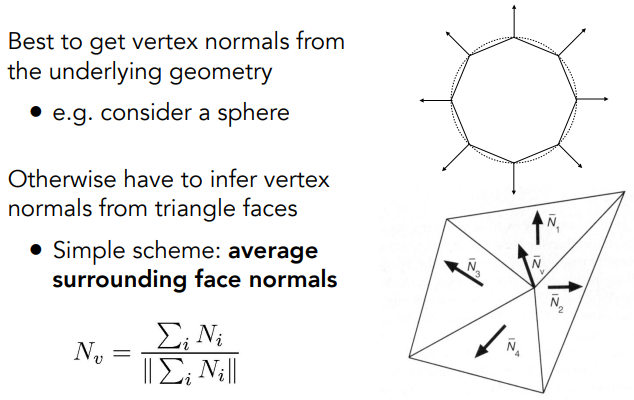

定义逐像素的法线

所有的法线都是方向，求出来之后需要归一化变成单位向量。利用重心坐标差值（后面讲）根据顶点法线求内部像素的法线。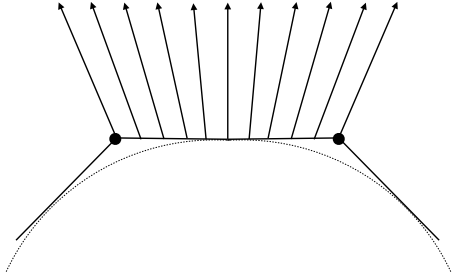

图形（实时渲染）管线 Graphics (Real-time Rendering) Pipeline

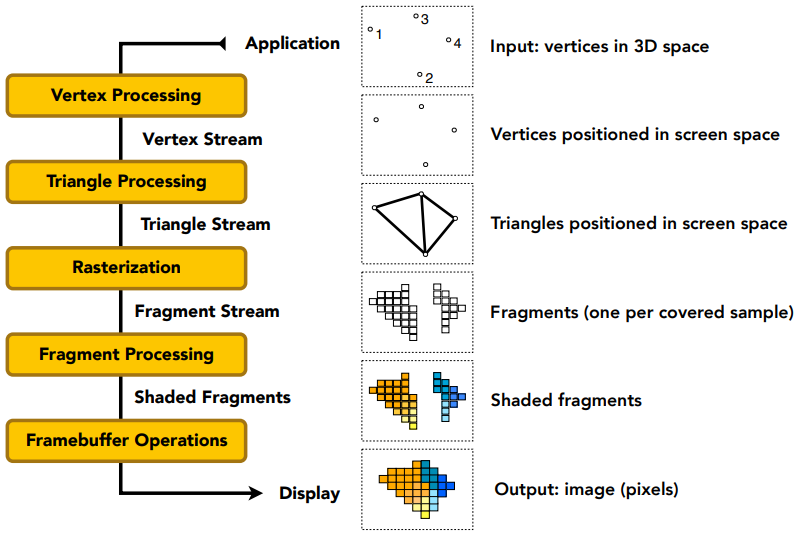
从三维场景到最后渲染出二维的一幅图的基本操作：

这个操作是已经在硬件里面写好的，gpu 里进行基本就是这个操作

• 顶点的处理 Vertex Processing
  • 输入一些空间中的点
  • MVP & Viewport 变换，将这些点投影到屏幕上
• 三角形的定义 Triangle Processing
  • 在屏幕上的这些点形成三角形

  为什么先将顶点投影在屏幕上就得到了三角形？
  比如 obj 模型文件，存储模型中所有的点信息，再存储每个三角面片由哪三个顶点组成，而将顶点投影到屏幕上后，顶点和三角面片的对应关系是不变的。

• 光栅化 Rasterization（包括 Fragment Processing）
  • 采样、做深度测试，找到在屏幕中能显示出来的像素
  • 把三角形画在屏幕上，用离散的 fragment（类比于像素）表示
• 着色 Shading
  • 对光栅化结果得到的 fragments 着色
  • 最后就输出得到一个图像 image (pixels)
    

顶点处理阶段，每个顶点做 MVP 变换：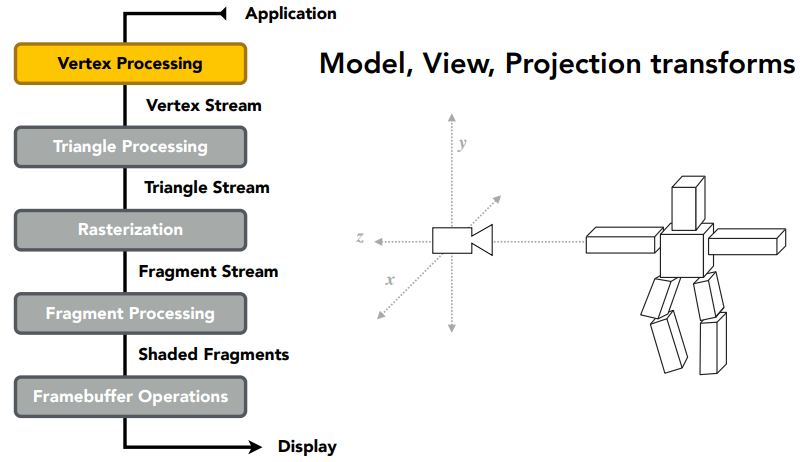

光栅化阶段，采样三角形的覆盖范围：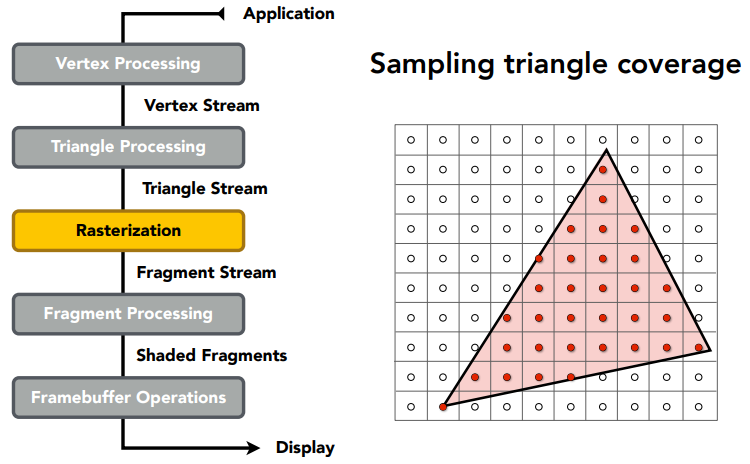

光栅化产生了一系列的 fragment 或 pixel，要判定是否可见（Z-Buffer），发生在 Fragment Processing 阶段，也可以把它归为光栅化阶段的一部分：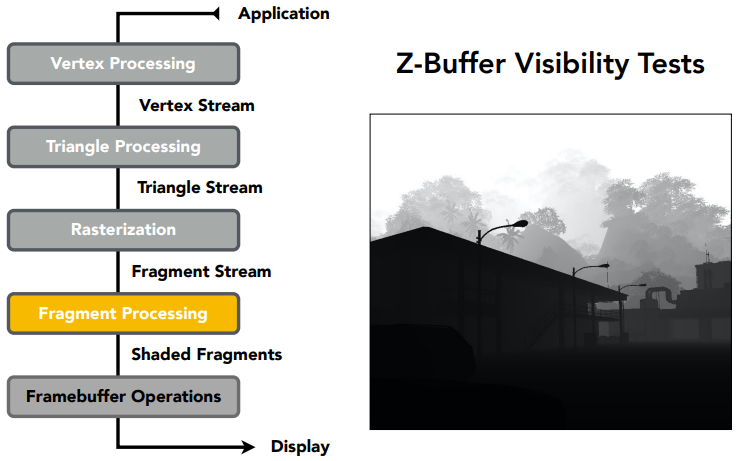

着色阶段，考虑到不同的着色频率，如果是 Gouraud shading 逐顶点着色，着色就发生在 Vertex Processing；如果是 Phong shading 逐像素着色，就要等像素都产生，所以在 Fragment Processing。

重要的是，如果想做着色，就是顶点、像素如何着色，在现代 gpu 里面，这一套渲染管线，Vertex Processing、Fragment Processing 是可编程的，这部分代码我们就叫做 shader，就是控制顶点和像素是如何着色的。

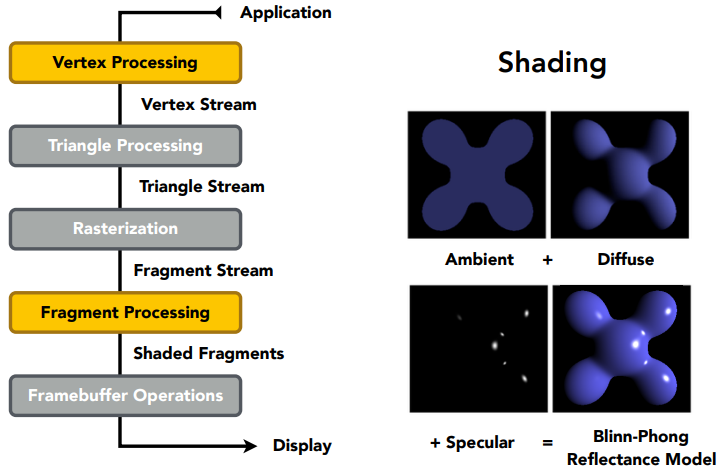
如何定义三角形内部每一个像素都拥有一个完全不同的属性（比如颜色），如下图，这就叫做纹理映射。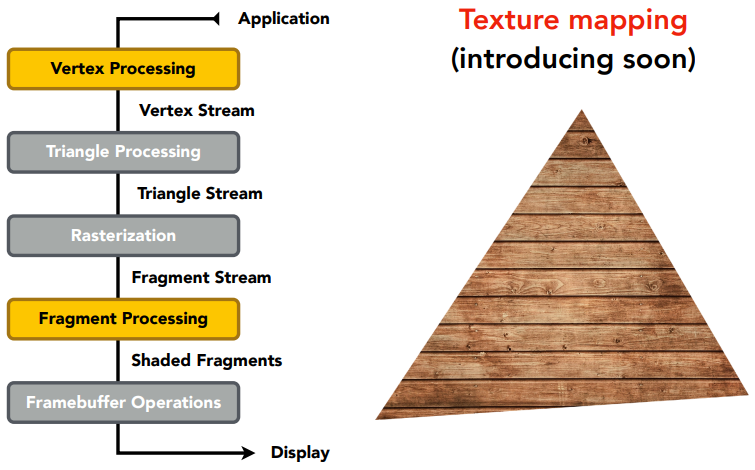

着色器程序 Shader Programs

• Vertex Processing、Fragment Processing 是可编程的
• 描述每个顶点或像素上的操作，控制如何着色

shader 本质上是一些能在硬件上执行的语言，比如 OpenGL（一个图形学的API）可以用来写一些 shader。shader 是一个通用的程序，会对每一个顶点或fragment或像素都执行一次，不需要自己写循环，在 shader 里面只需要管一个顶点或像素怎么操作就可以了。

如果写的是顶点的操作，就叫做 vertex shader，顶点着色器；如果是像素的操作，就叫做 fragment/pixel shader，片段/片元/像素着色器。

下面是一个简单的 openGL 的一个着色语言，简称 GLSL，写的一个片元着色器程序示例：

uniform sampler2D myTexture;    // program parameter
uniform vec3 lightDir;          // program parameter
varying vec2 uv;                // per fragment value (interp. by rasterizer)
varying vec3 norm;              // per fragment value (interp. by rasterizer)

void diffuseShader() {
    vec3 kd;
    kd = texture2d(myTexture, uv);                  // material color from texture
    kd *= clamp(dot(–lightDir, norm), 0.0, 1.0);    // Lambertian shading model
    gl_FragColor = vec4(kd, 1.0);                   // output fragment color
}

该着色器执行纹理查找以获得此时表面的材质颜色，然后执行漫反射照明计算。

推荐网站 shadertoy
Inigo Quilez, https://www.shadertoy.com/view/ld3Gz2