Rasterization 2 (Antialiasing and Z-Buffering)

抗锯齿 Antialiasing

• 采样在计算机图形学中无处不在

  • Rasterization = Sample 2D Positions
    
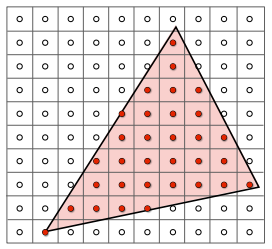
  • Photograph = Sample Image Sensor Plane
    
  • Video = Sample Time
    

• 计算机图形学中的采样瑕疵 Sampling Artifacts (Errors / Mistakes / Inaccuracies)

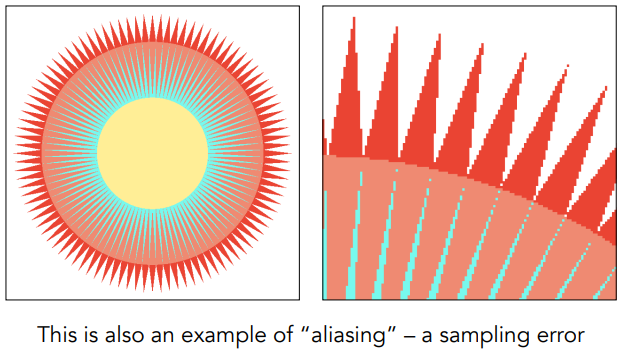
  • 锯齿 Jaggies (Staircase Pattern)
    
  • 摩尔纹 Moiré Patterns in Imaging

  把左图的奇数行和奇数列都去掉，缩小得到右图

  

  • 马车车轮错觉（假动）Wagon Wheel Illusion (False Motion)

  人眼在时间中的采样跟不上运动的速度

  

• 采样造成的瑕疵 - “走样” Artifacts due to sampling - “Aliasing”

  • 锯齿 Jaggies – 对空间采样 sampling in space
  • 摩尔纹 Moire – 欠采样图像 undersampling images
  • 马车车轮效应 Wagon wheel effect – 对时间采样 sampling in time

• Aliasing Artifacts （走样瑕疵）的背后

  • 信号变化太快（高频），但采样太慢

• Antialiasing 反走样（抗锯齿）思路：采样前模糊 Blurring（预滤波 Pre-Filtering）

  • 光栅化三角形中的锯齿，其中像素值为纯红色或白色
    
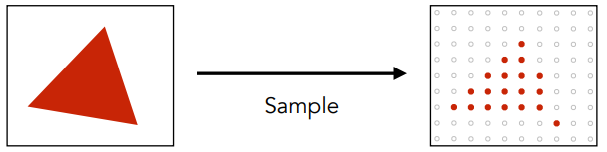
  • 光栅化三角形中的抗锯齿边缘，其中像素值采用中间值

  对三角形先做模糊处理，再进行采样

  

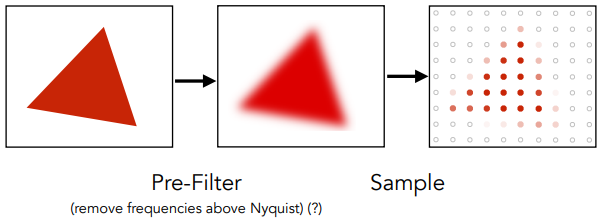
  • 对比 Point Sampling vs Antialiasing
    
    
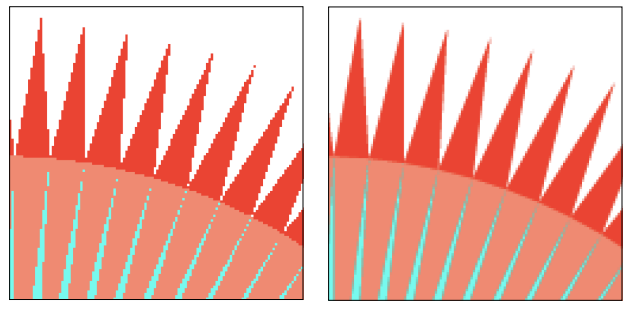
  • 能不能先采样再模糊？不能
    

• 但是为什么？

  • 为什么欠采样会导致走样/锯齿？
  • 为什么先预滤波再采样可以做到抗走样/锯齿？

下面会深入探讨根本原因并看看如何实现抗锯齿光栅化。

采样理论 Sampling theory

频域 Frequency Domain

正弦和余弦函数 Sines and Cosines

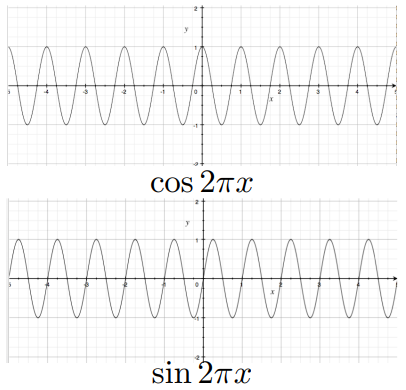
频率 Frequencies

频率 f 越大，信号变化越快，周期 T 越短

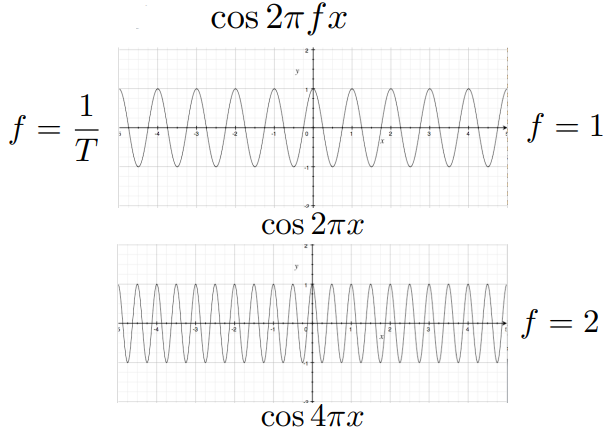
傅立叶变换 Fourier Transform

傅里叶级数展开，任何一个周期函数都可以表示为一系列正弦和余弦的加权和

加更多的项，做更近似的拟合

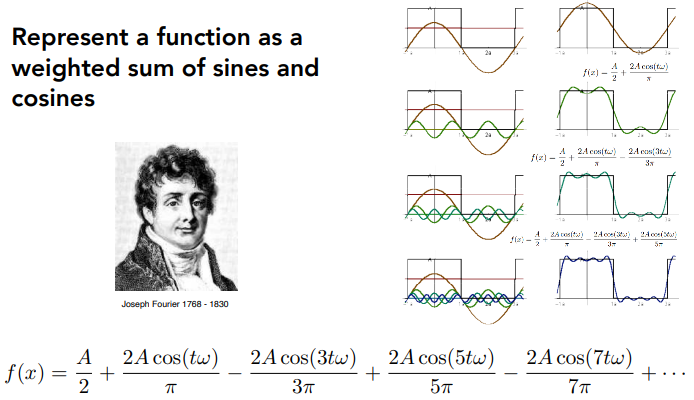
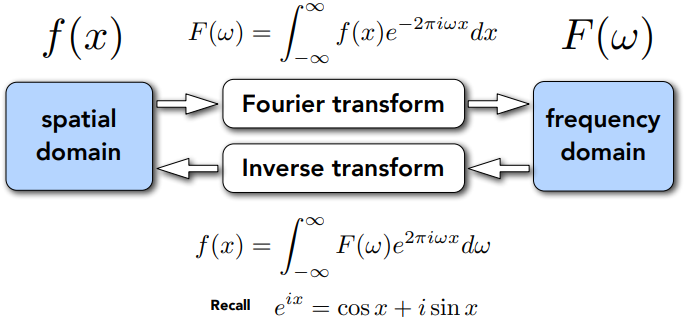
傅立叶变换将信号 Signal 分解为频率 Frequencies。

将一个函数经过复杂操作后变成另外一个函数（不同频率的段），通过逆变换还能变回来，这个操作就叫傅里叶变换和逆傅里叶变换

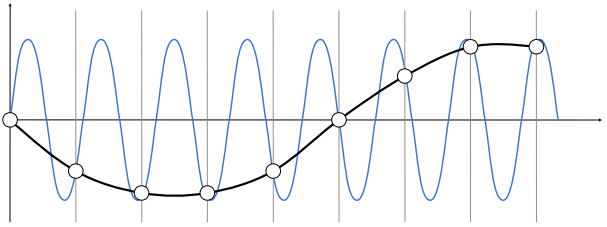
更高的频率需要更快的采样（高频信号采样不足，不能正确恢复信号

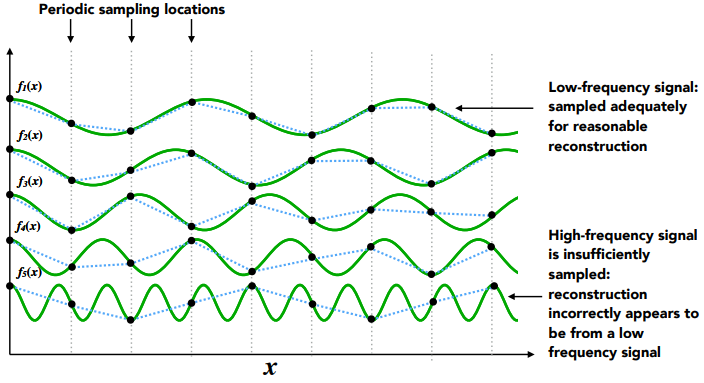
欠采样会产生频率走样。

两个不同频率的信号经过相同的采样后得到的结果无法区分。高频信号采样不足，样本错误地显示为来自低频信号，在给定采样率下无法区分的两个频率称为 “Aliases 混叠/叠频”。

滤波 Filtering

Filtering = Getting rid of certain frequency contents 去除某些频率的内容

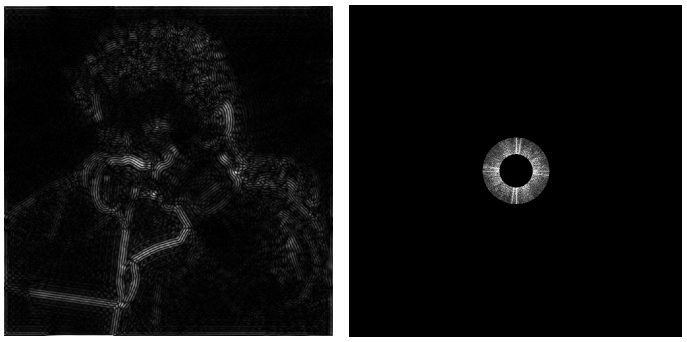
将图像的频率内容可视化

右图从中心到周围，频率越来越高；在不同频率有多少信息，用亮度表示

右图中比较明显的水平和竖直线是因为：
我们在分析一个信号的时候，会认为是一个周期性重复的信号，对不周期性重复的比如这张图，就认为这张图其实一直在平铺重复，而因为图片左右边界和上下边界变化较大，会发生剧烈的信号变化，产生高频。
为了分析图内部的信息，忽略这两条线就行。

傅里叶变换能够让我们看到，任何信号（比如一个图像）在不同的频率下的信息，我们叫它频谱。

滤除低频（高通滤波器），图片只剩下了边界（轮廓）

信号变化大的地方，就是高频信息

滤除高频（低通滤波器），图片变得模糊

滤除低频和高频，留下某一段的频率

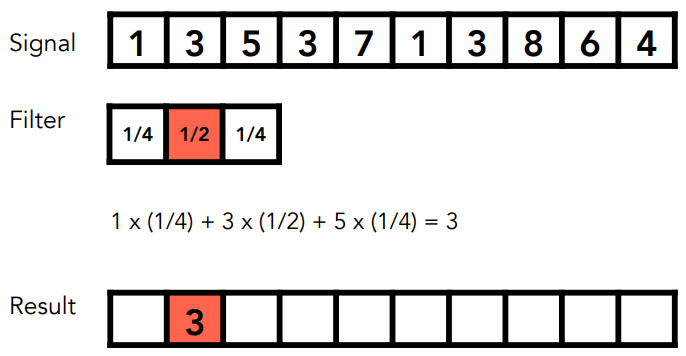
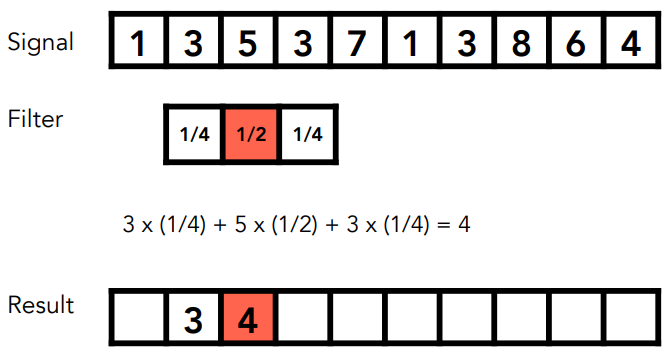
Filtering = Convolution (= Averaging) 卷积

卷积理论 Convolution Theorem

空间域/时域 spatial domain 的卷积 Convolution 等于频域 frequency domain 的乘法 multiplication，反之亦然。

• Option 1:
  • 在空间域中通过卷积进行过滤
• Option 2:
  • 变换到频域（傅里叶变换）
  • 乘以卷积核（滤波器）的傅里叶变换
  • 变换回空间域（傅里叶逆变换）
    

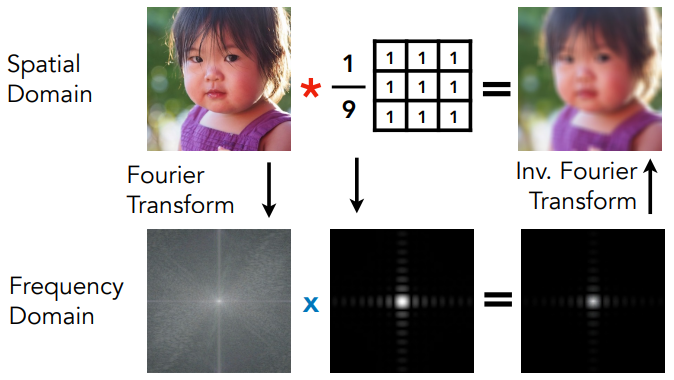
Box Filter

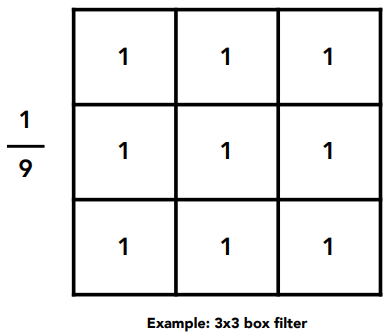
Box Function = “Low Pass” Filter

Wider Filter Kernel = Lower Frequencies（更宽的滤波器内核 = 更低的频率

时域中的卷积核变大了，对应的频域图变小了
用越大的Box，得到的结果越模糊，频率范围越小（只能留下更低的频率

采样 Sampling = Repeating Frequency Contents 重复频率内容

采样（时域上）：原始信号 (a) 乘上周期冲激函数 (c) ，得到采样结果 (e)
时域上的乘积等于频域上的卷积，也就对应频域上 (b) 与 (d) 的卷积结果是 (f)
这样可以看出，采样在频域上，就是把原来的频谱复制粘贴（采样就是在重复一个原始信号的频谱

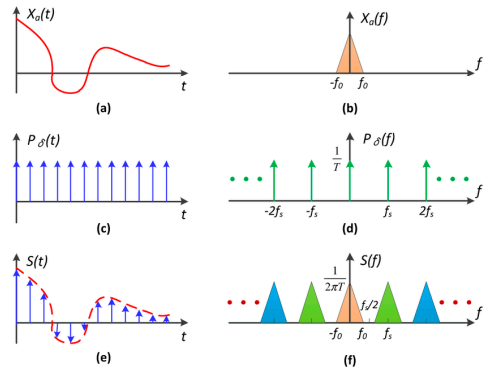
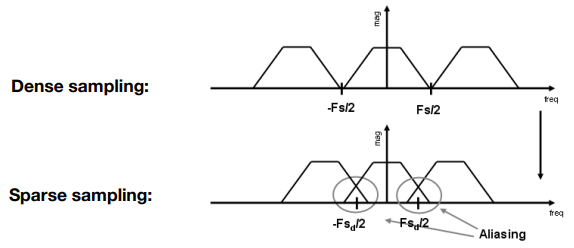
混叠/走样 Aliasing = Mixed Frequency Contents 混合频率内容

采样率不足，采样的不够快，原始信号频谱重复的中间间隔就会非常小，对应下图稀疏采样 Sparse sampling
因为冲激函数在频域里的间隔是时域的倒数，所以时域越宽（采样间隔大），频域越窄（频谱的重复间隔小）
看上图，时域的横轴是时间，也就是周期，频域的横轴是频率，而周期是频率的倒数

抗锯齿 Antialiasing

如何减少 Aliasing Error ？

• Option 1: Increase sampling rate 提高采样率

  • 实质上增加了傅里叶域（频域）中 replicas 副本/复制品（重复的信号频谱）之间的距离
  • 更高分辨率的显示器、传感器、帧缓冲区……
    但是：成本高并且可能需要非常高的分辨率（而且反走样的目的就是对同一个屏幕而言，不受制于物理限制

• Option 2: Antialiasing 反走样/抗锯齿

  • 频域上，在重复频谱之前使原始信号的频谱“变窄”
  • 例如：采样前滤除高频
    
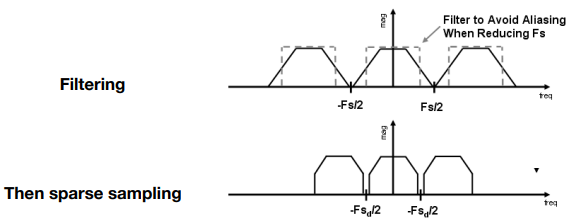
  • 上面我们提到的“模糊处理”就是一种预滤波 Pre-Filter
    
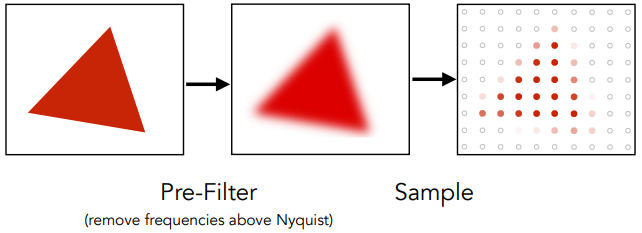
  • 一个实用的预滤波 Pre-Filter：A 1 pixel-width box filter (low pass, blurring)

  用来模糊处理，就是一个低通滤波器，下图左时域（滤波器/卷积核）、右频域

  

Antialiasing by Computing Average Pixel Value

计算平均像素值抗锯齿：

• 用 1-pixel box-blur 对 f(x, y) 卷积 Convolve
• 然后在每个像素的中心采样
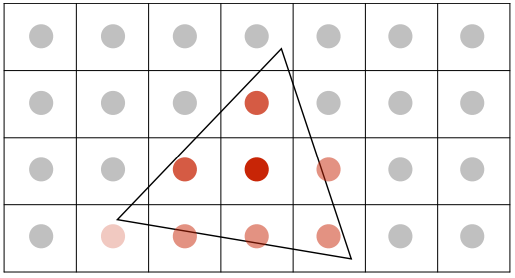
• 在光栅化一个三角形时，f(x,y) = inside(triangle,x,y) 的像素区域内的平均值等于三角形覆盖的像素面积
  

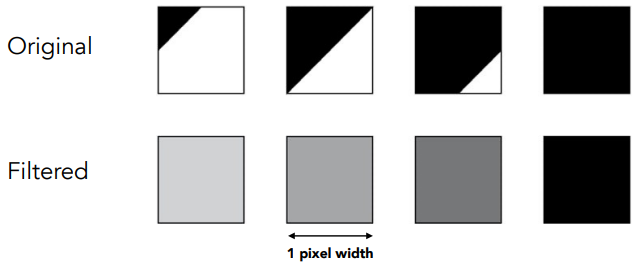
Antialiasing By Supersampling (MSAA)

实际上计算每一个像素的平均值（求这个像素被三角形覆盖的面积），这并不简单，而且计算量很大，于是我们采用近似处理的方法。超采样抗锯齿：
对一个像素内的多个位置进行采样，并对它们的值求平均值，来近似 1 像素盒式滤波器（1-pixel box filter）的效果：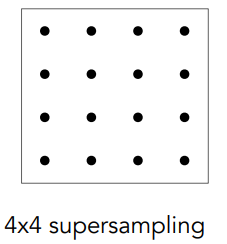

单点采样：每个像素是一个采样点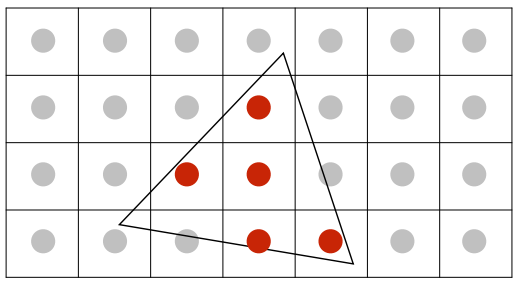

超采样：

1. 在每个像素中获取 NxN 个采样点：
   
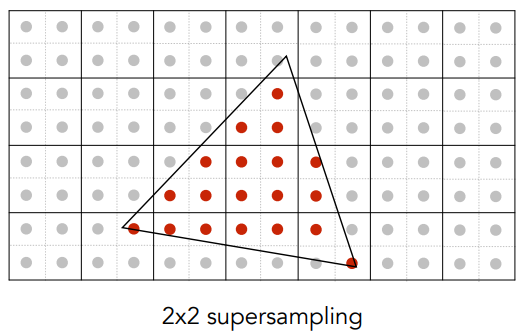
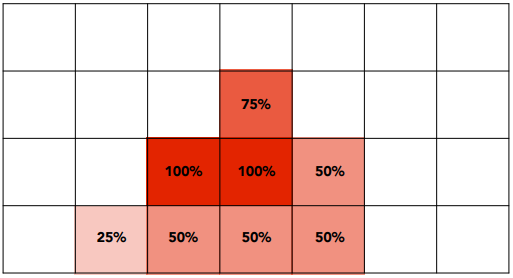
2. 对每个像素内的 NxN 个样本值求平均：
   
   
   
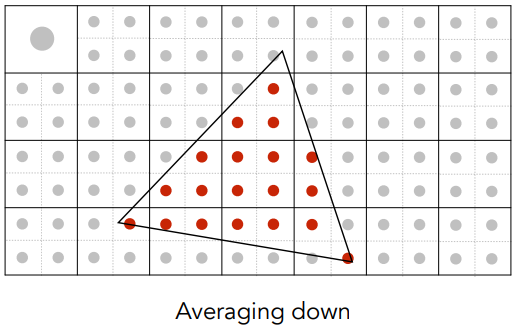
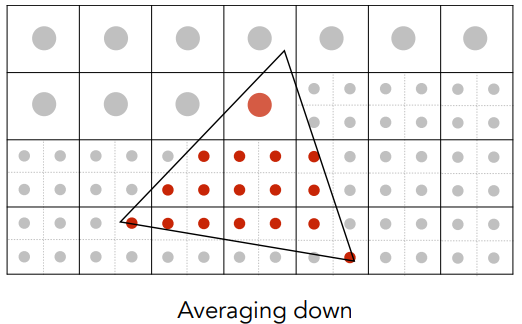
3. 超采样的结果：这是显示器发出的相应信号
   
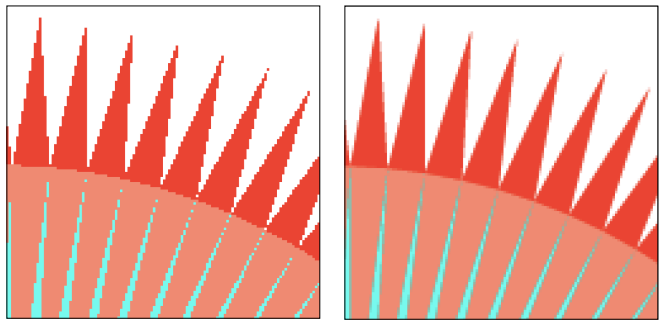
4. 单点采样和 4x4 超采样对比：
   

把一个像素细分为 NxN 个更小的次像素，以分出来的次像素值求平均表示该像素的值，就像模拟在一个高分辨率屏幕下的光栅化，再进行像素合并（取平均）变为低分辨率下的光栅化，这是 SSAA。
但是 MSAA 并不是通过提高分辨率来解决问题的，只是为了通过这些采样点来检测三角形的覆盖。

超级采样抗锯齿 （Super-Sampling Anti-Aliasing，简称SSAA）
古老的全图抗锯齿。把图片放进缓存并放大，把放大后的图像像素采样临近2个或4个像素，混合，生成的最终像素，令图形的边缘色彩过渡趋于平滑，最后把图像还原回原来大小。缺点：很吃性能。

多重采样抗锯齿（Multi-Sampling Anti-Aliasing，简称MSAA）
首先来自于OpenGL。具体是 MSAA 只对 Z 缓存（Z-Buffer）和模板缓存 (Stencil Buffer) 中的数据进行超级采样抗锯齿的处理。可以简单理解为只对多边形的边缘进行抗锯齿处理。相比SSAA对画面中所有数据进行处理，MSAA对资源的消耗需求大大减弱（优点），不过在画质上可能稍有不如SSAA（缺点）。

MSAA 和 SSAA 的区别？
https://www.zhihu.com/question/20236638

现代抗锯齿 Antialiasing Today

• MSAA 的代价是什么？

理论上增大了 NxN 倍的计算量（目前只考虑在光栅化阶段），实际上并不会对像素进行规则划分，工业上利用更加有效图案来分布采样点，有一些采样点还会被邻近的不同像素所复用，所以我们玩游戏时，假如开启 4 倍 MSAA 抗锯齿，帧率并不会掉到原来的四分之一（实际上渲染也不是只有光栅化阶段）。

• 里程碑 Milestones (personal idea)
  • FXAA (Fast Approximate AA)
  • TAA (Temporal AA)
• 超分辨率 Super resolution / super sampling
  • From low resolution to high resolution
  • Essentially still “not enough samples” problem
  • DLSS (Deep Learning Super Sampling)

可见性 / 遮挡 Visibility / occlusion

之前提到的光栅化都只考虑对一个三角形，实际场景由好多三角形组成，各自离相机的距离不一样，如何把这些三角形都画在屏幕上，并且它们的遮挡关系是对的：近处的永远要遮住远处的，这就是可见性/遮挡的问题。

画家算法 Painter’s Algorithm

受到画家如何从后到前绘画的启发，在帧缓冲区（frame buffer）中覆盖 overwrite

先画（光栅化）远处的物体，然后再画（光栅化）近处的物体来覆盖远处的物体

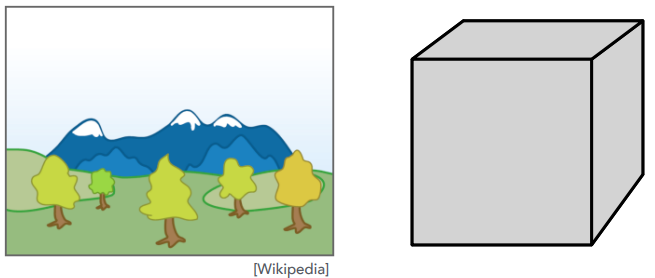
需要对深度排序 (对 n 个三角形的深度排序为 O(nlogn))，可能有无法解析的深度顺序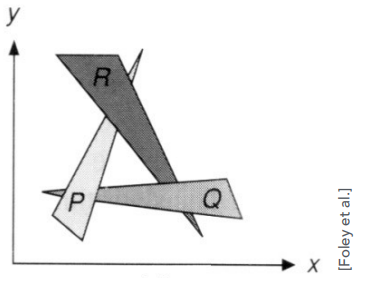

深度缓存 Z-buffering

This is the algorithm that eventually won.

• 存储每个样本（像素）的当前最小 z 值（找最近的样本
• 需要额外的深度值缓冲区
  • 帧缓冲区（frame buffer）存储颜色值
  • 深度缓冲区（z-buffer）存储深度

重要提示：为简单起见，我们假设 z 始终为正
（较小的 smaller z -> closer 较近，较大的 larger z -> further 较远）

Z-buffer 算法

初始化深度缓冲区为无穷远 ∞，光栅化期间：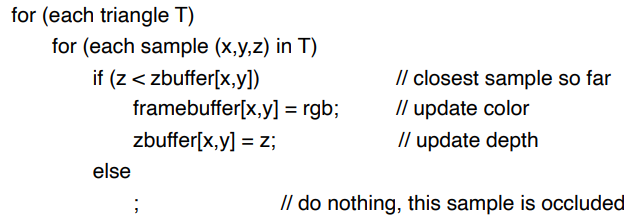

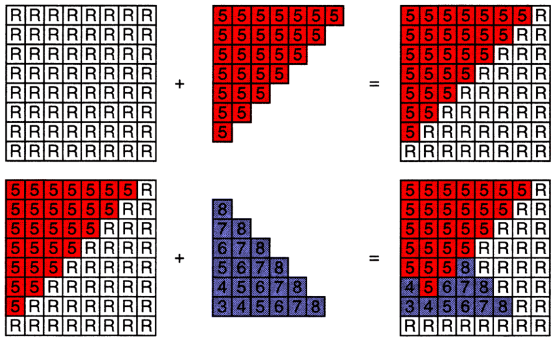
画家算法是对所有三角形的深度排序，而深度缓存是（遍历所有三角形）对每一个被三角形覆盖的像素按最近深度同时更新颜色和深度。每个三角形不同的位置有不同的深度，这个后面会说如何计算。根据像素的深度比较，如果有更近的，同时更新颜色值（frame buffer）和深度值（z-buffer）

Z-Buffer 复杂度 Complexity

• n 个三角形时间复杂度 O(n)（假设三角形覆盖的像素数为一个常数）
• 这里并不是在排序，只是记录最小值

假设不会出现两个不同的三角形在一个像素上有相同的深度，深度缓存算法与所有三角形遍历绘制的顺序无关。

深度缓存 z-buffer 算法是非常重要的可见性算法，广泛应用在几乎所有 GPU 硬件中。

目前来说所有的光栅化都会做一个深度的测试，每个像素都维护一个这样的一个深度的测试，就可以得到正确的遮挡算法。对 MSAA（包括SSAA）来说，z-buffer 是对每一个采样点而不再是每一个像素维护一个深度值。但是 z-buffer 处理不了透明物体。