Rasterization 1 (Triangles)
结束观测变换 Finishing up Viewing
透视投影 Perspective Projection
近平面的 l, r, b, t 是什么?
- 定义一个视锥,从相机到近平面
- vertical field-of-view (fovY) and aspect ratio
- 垂直视场(可视角度)和宽高比(假设是对称的,则 l = -r, b = -t)
通过宽高比和垂直的可视角度,可以推出水平的可视角度
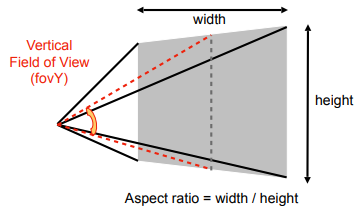
如何从 fovY 和 aspect ratio 转换到 l, r, b, t ?
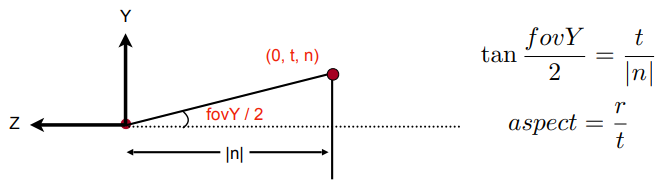
视口变换 Viewport transformation
MVP变换之后是什么?
- Model transformation (placing objects)
- View transformation (placing camera)
- Projection transformation
- Orthographic projection (cuboid to “canonical” cube )
- Perspective projection (frustum to “canonical” cube)
- Canonical cube to ?
规范立方体到屏幕 Canonical Cube to Screen
- What is a screen?
- An array of pixels
- Size of the array: resolution(分辨率)
- A typical kind of raster display
- Raster(光栅)== screen in German
- Rasterize(光栅化)== drawing onto the screen
- Pixel (FYI, short for “picture element”)
- For now: A pixel is a little square with uniform color
- Color is a mixture of (red, green, blue)
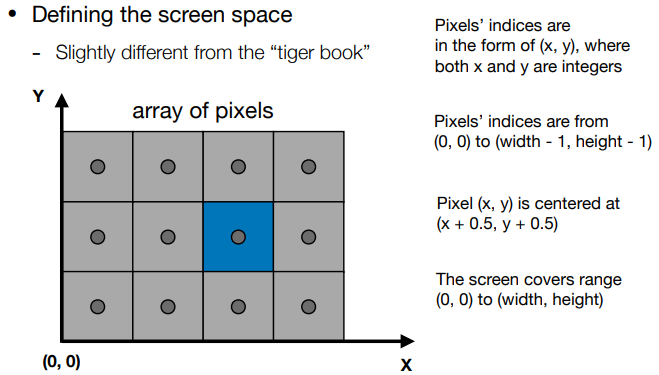
- 定义屏幕空间(与《Fundamentals of Computer Graphics》略有不同
- 像素索引的形式为 (x, y),其中 x 和 y 都是整数
- 像素索引 from (0, 0) to (width - 1, height - 1)
- 像素 (x, y) 的中心是 (x + 0.5, y + 0.5)
- 屏幕覆盖范围 (0, 0) to (width, height)
- 与 z 轴无关,xy 平面中的变换: to
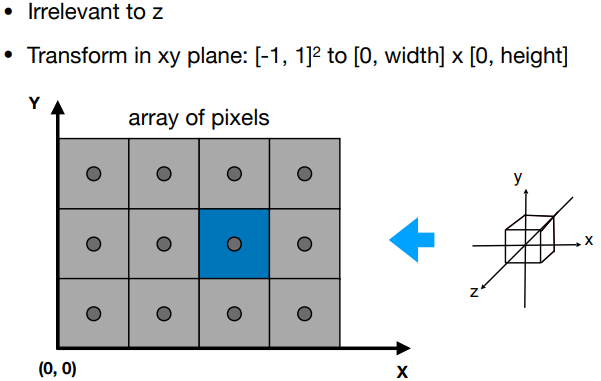
- 视口变换矩阵 Viewport transform matrix:
光栅化 Rasterization
不同的光栅显示 Different raster displays
- 示波器 Oscilloscope
- 阴极射线管 Cathode Ray Tube (CRT)
- 电视 Television - 光栅显示 CRT(光栅扫描:p逐行扫描,i隔行扫描…
- 帧缓冲区 Frame Buffer:用于光栅显示的内存
- 平板显示器 Flat Panel Displays(低分辨率液晶显示屏 Low-Res LCD Display
- LED 阵列显示屏 LED Array Display
- 电泳(电子墨水)显示器 Electrophoretic (Electronic Ink) Display
光栅化三角形 Rasterizing a triangle
光栅化:绘图到光栅显示 Rasterization : Drawing to Raster Displays
- 多边形网格 Polygon Meshes

- 三角形网格 Triangle Meshes
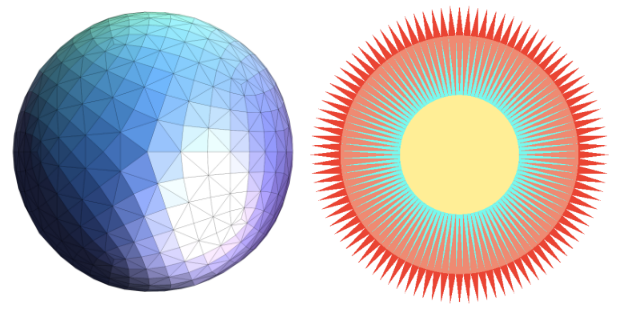
- 三角形 - 基本形状基元 Triangles - Fundamental Shape Primitives
- 为什么是三角形?
- 最基本的多边形
- 分解其他多边形
- 独特的属性
- 内部一定是平面的
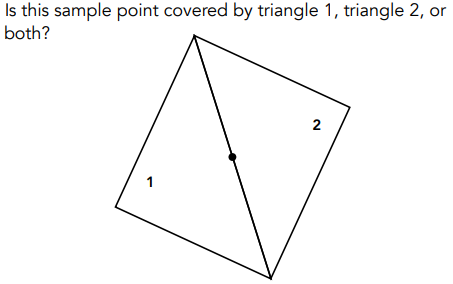
- 内部外部定义明确(向量叉积判断一个点是否在三角形内
- 定义明确的在三角形顶点处插值的方法(重心插值)
- 最基本的多边形
- 为什么是三角形?
- 什么像素值近似于三角形(如何用像素近似表达一个三角形)?
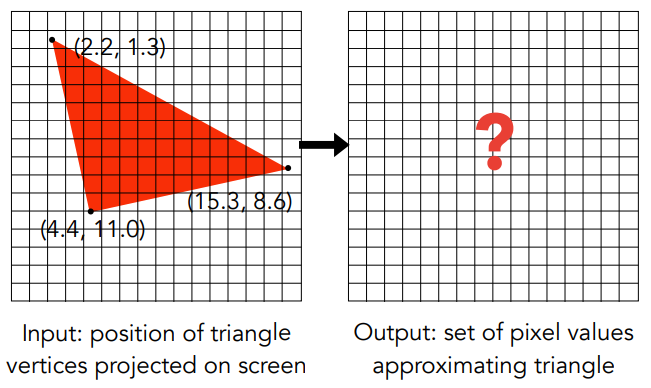
采样 A Simple Approach: Sampling
对函数进行采样 Sampling a Function
在某个点评估函数就是采样。Evaluating a function at a point is sampling.
我们可以通过采样来离散函数。We can discretize a function by sampling.
1 | for (int x = 0; x < xmax; ++x) |
采样是图形学的核心思想。
我们采样时间 time (1D),面积 area (2D),方向 direction (2D),体积 volume (3D)…
光栅化是 2D 采样,利用像素中心对屏幕空间进行采样。
如果像素中心在三角形内(Each Pixel Center Is Inside Triangle),则进行采样。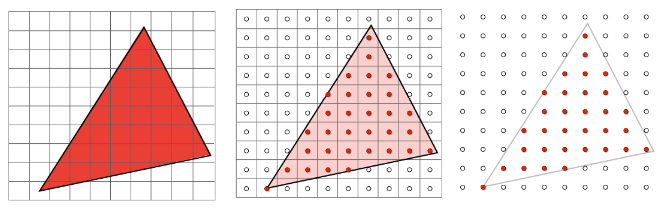
定义二元函数:bool inside(tri, x, y),x, y 不一定是整数。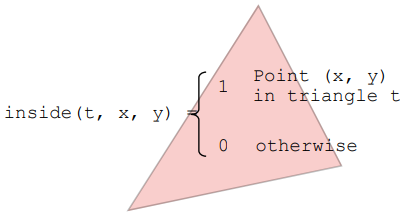
Rasterization = Sampling A 2D Indicator Function
二元函数 inside(tri, x, y) 中 x, y 是连续变量,通过采样(像素中心)来离散函数。
1 | // 对所有像素遍历 |
inside(tri, x, y)
可以利用向量叉积判断一个点(像素中心)是否在三角形内,来实现 inside 函数。
对于点刚好在三角形边上的情况,可以自行定义该点是否在三角形内。
通常对于这样的问题,要么不做处理,要么特殊处理。
在这门课上,我们不做处理。
在一些图形学API中,比如 OpenGL、DirectX,会有非常严格的规定,比如上边和左边的点认为在三角形内,右边和下边的点认为不在三角形内,了解即可。
光栅化加速
考虑一个三角形的光栅化时,没必要检查屏幕上的所有像素。
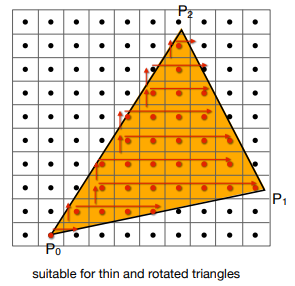
可以根据三角形顶点坐标范围定义一个包围盒 Bounding Box,只考虑这个区域内的像素: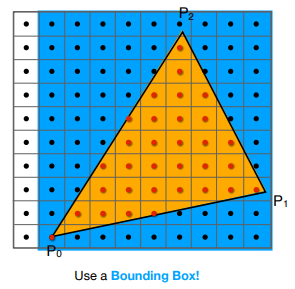
增量三角形遍历 Incremental Triangle Traversal (Faster?)
每一行都找它的最左和最后,当然做起来不是很容易
适用于细三角形和旋转三角形,包围盒覆盖像素比实际覆盖像素多很多
现实显示器的光栅化
真实液晶屏像素,注意 R、G、B 像素几何结构。
彩色打印:观察半色调图案。(CMYK
假设显示像素发射方形光:笔记本电脑上的 LCD 像素实际上并不以均匀颜色的正方形发光,但这种近似值足以满足我们当前的讨论。(这门课上仍然认为一个像素就是一个颜色均匀的小方块
走样 Aliasing(锯齿 Jaggies)
最后,如果我们向显示器发送采样信号,显示器实际显示: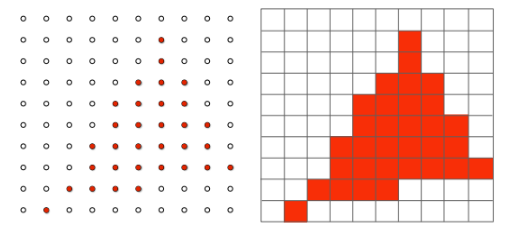
对比连续的三角形,会出现锯齿,因为像素本身有一定大小,采样率对信号来说不够高,所以产生了这样的信号走样问题。
走样问题,在光栅化图形学上就体现在锯齿上: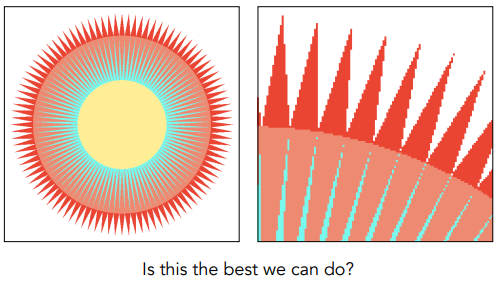
之后会介绍反走样、抗锯齿等