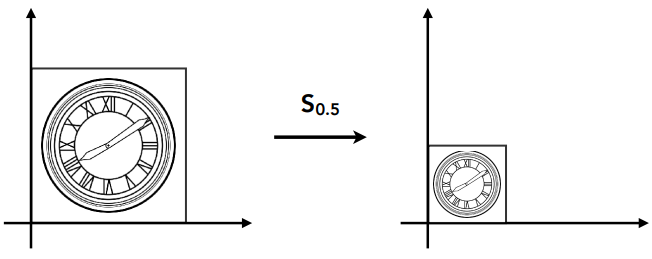
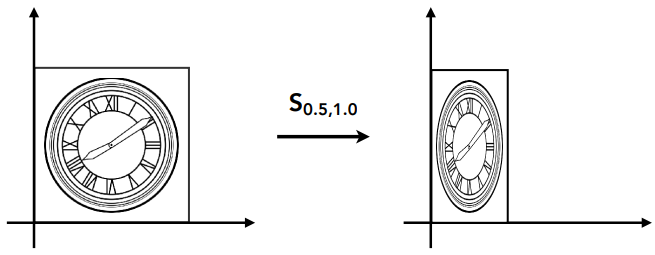
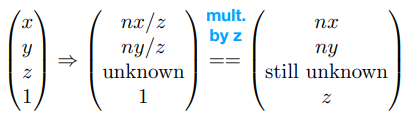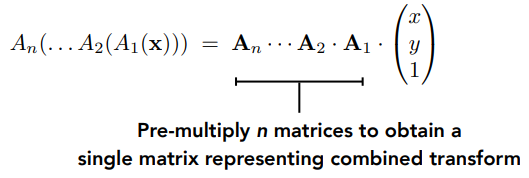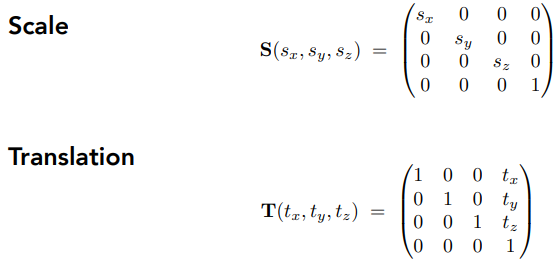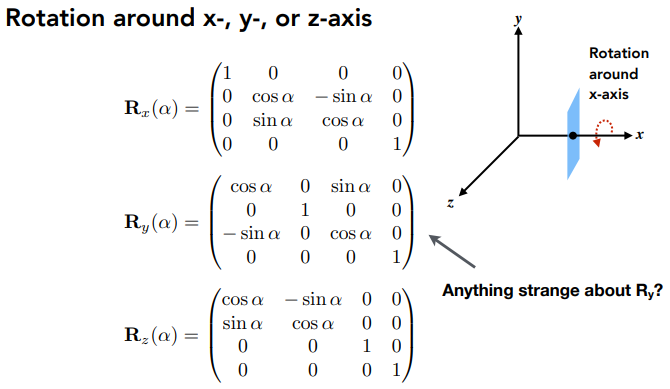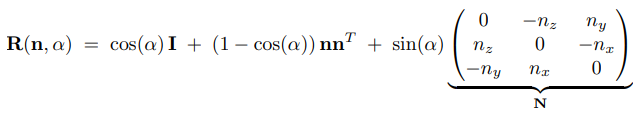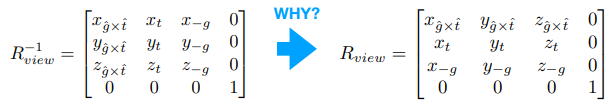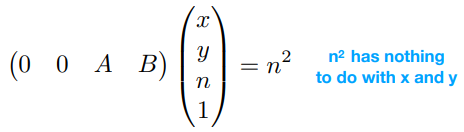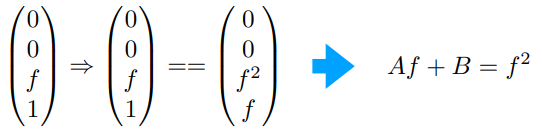缩放 Scale
- Transform: x′=sxx;y′=syy
- Matrix: [x′y′]=[sx00sy][xy]
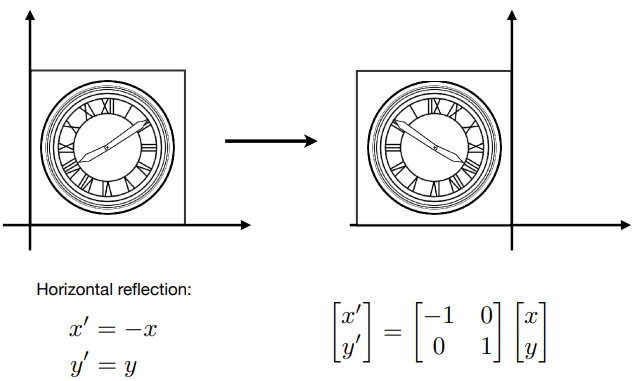
Reflection Matrix
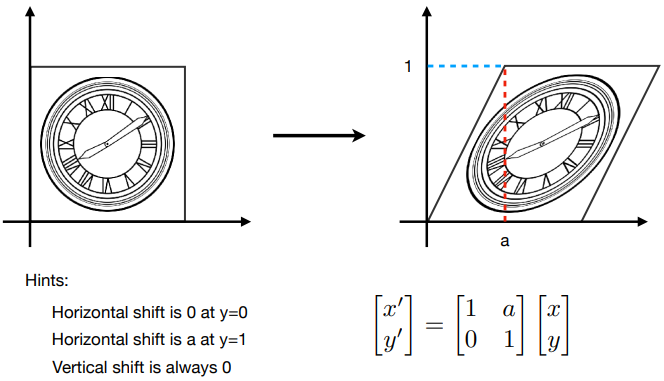
Shear Matrix
旋转 Rotate
- 默认绕 (0, 0) ,逆时针(Counterclockwise)旋转
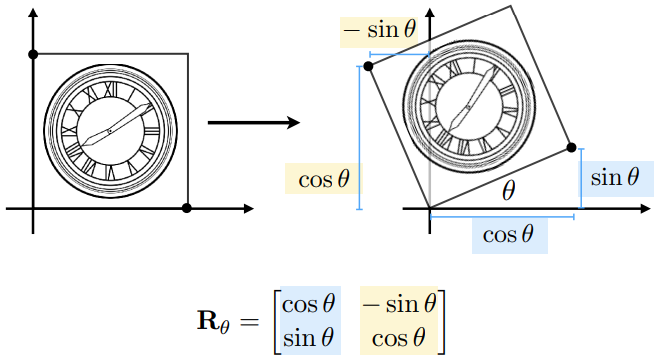
Rθ 矩阵推导:
设 x′=Rθx,即 [x′y′]=[acbd][xy]
由特殊点:
( cosθ, sinθ) ← (1, 0) 得 a = cosθ, c = sinθ ;
(-sinθ, cosθ) ← (0, 1) 得 b = -sinθ, d = cosθ 。
x′=ax+byy′=cx+dy [x′y′]=[acbd][xy] 平移 Translation
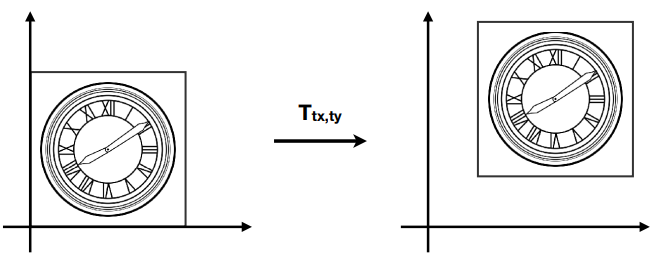
x′=x+txy′=y+ty [x′y′]=[acbd][xy]+[txty] 平移不能以矩阵形式表示,不是线性变换。但是我们不希望平移成为一种特殊情况。
是否有一个统一的方式来表示所有的变换?(代价是什么?)
齐次坐标 Homogeneous coordinates
添加第三个坐标:w
- 2D point = (x,y,1)T
- 2D vector = (x,y,0)T
平移的矩阵表示: ⎣⎡x′y′w′⎦⎤=⎣⎡100010txty1⎦⎤⋅⎣⎡xy1⎦⎤=⎣⎡x+txy+ty1⎦⎤
如果平移一个向量会怎样?
向量只关注长度、方向,经过平移之后保持不变。
w = 1,表示一个点 point,w = 0 表示一个向量 vector:
- vector + vector = vector
- vector - vector = vector + (-vector)
- point + vector = point
- point - vector = point + (-vector)
- point + point = ???
- point - point = vector
当 point + point 时,结果的 w = 2,我们规定在齐次坐标中:
(x,y,w)Tisthe2Dpoint(wx,wy,1)T,w=0 所以齐次坐标中,两点相加得到的是两点的中点 point + point = (mid) point。
- 先线性变换,再平移(Affine map = linear map + translation
[x′y′]=[acbd][xy]+[txty] ⎣⎡x′y′1⎦⎤=⎣⎡ac0bd0txty1⎦⎤⋅⎣⎡xy1⎦⎤ 
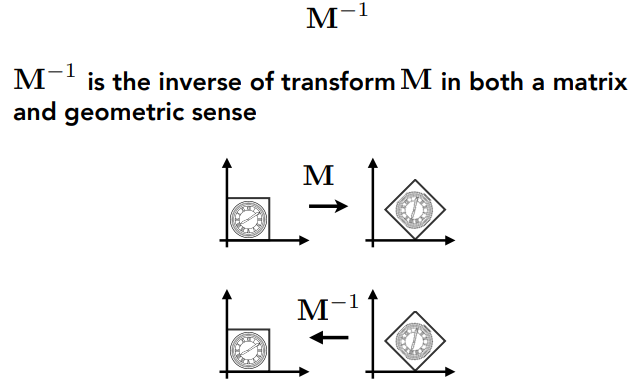
x=Ix=M−1Mx=M−1x′ 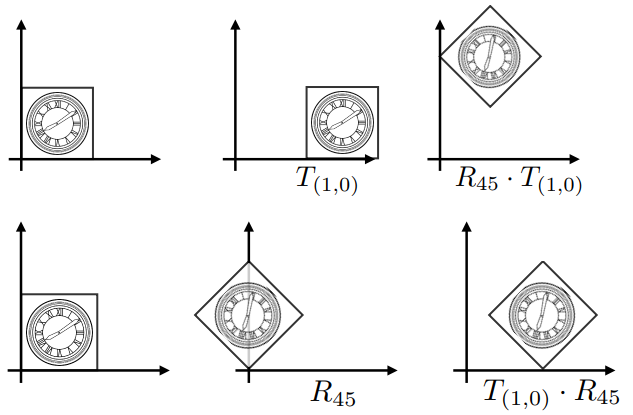
R45⋅T(1,0)=T(1,0)⋅R45 T(1,0)⋅R45⎣⎡xy1⎦⎤=⎣⎡100010101⎦⎤⎣⎡cos45∘sin45∘0−sin45∘cos45∘0001⎦⎤⎣⎡xy1⎦⎤ 对仿射变换序列:A1,A2,A3,...,An,由矩阵乘法组成:
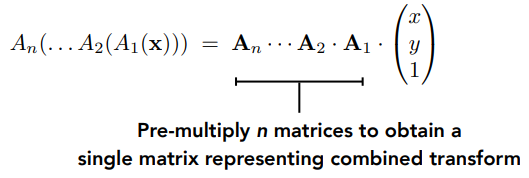
矩阵乘法虽然没有交换律,但是有结合律,预乘 n 个矩阵以获得表示组合变换的单个矩阵,这对性能来说非常重要。
⎣⎡x′y′1⎦⎤=⎣⎡100010txty1⎦⎤⎣⎡ac0bd0001⎦⎤⎣⎡xy1⎦⎤=⎣⎡ac0bd0txty1⎦⎤⎣⎡xy1⎦⎤ 我们之前说的旋转,是绕原点 (0, 0),如何绕给定的点 c 旋转?
- 将点 c 平移至原点;
- 旋转;
- 将点 c 平移回去。
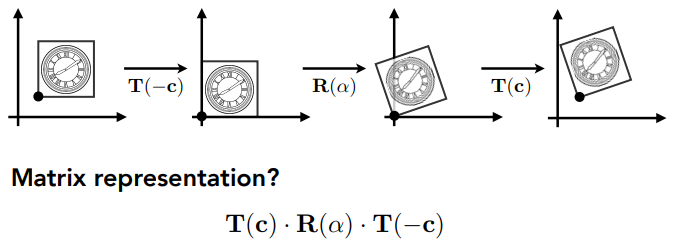
类比 2D 变换,使用齐次坐标:
- 3D point = (x,y,z,1)T
- 3D vector = (x,y,z,0)T
Ingeneral,(x,y,z,w)Tisthe3Dpoint(wx,wy,wz,1)T,w=0 使用 4×4 矩阵进行仿射变换(先线性变换,再平移):
⎣⎢⎢⎡x′y′z′1⎦⎥⎥⎤=⎣⎢⎢⎡100001000010txtytz1⎦⎥⎥⎤⋅⎣⎢⎢⎡adg0beh0cfi00001⎦⎥⎥⎤⋅⎣⎢⎢⎡xyz1⎦⎥⎥⎤=⎣⎢⎢⎡adg0beh0cfi0txtytz1⎦⎥⎥⎤⋅⎣⎢⎢⎡xyz1⎦⎥⎥⎤ 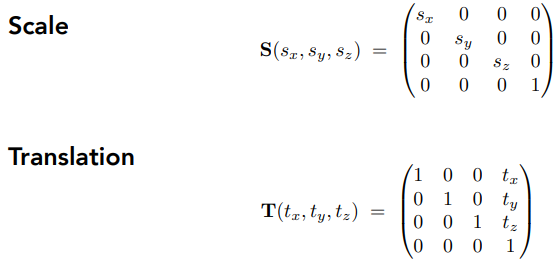
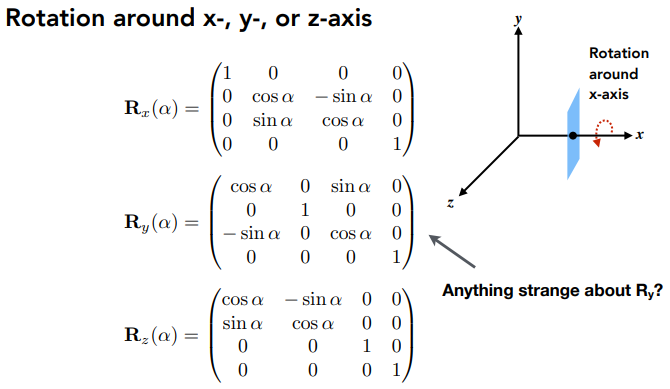
绕 x 轴旋转,x 坐标不变,y⇀×z⇀=+x⇀,在 y-z 平面旋转 θ,Rx(θ) 的 y, z 坐标矩阵与 2D 旋转矩阵 Rθ 相同;
绕 z 轴旋转,z 坐标不变,x⇀×y⇀=+z⇀,在 x-y 平面旋转 θ,Rz(θ) 的 x, y 坐标矩阵与 2D 旋转矩阵 Rθ 相同;
绕 y 轴旋转,y 坐标不变,z⇀×x⇀=+y⇀,在 z-x 平面旋转 θ,Ry(θ) 的 z, x 坐标矩阵与 2D 旋转矩阵 Rθ 相同;
但是因为我们矩阵坐标顺序为 x, y, z,所以实际是 Ry(θ) 的 x, z 坐标矩阵与 2D 旋转矩阵 Rθ−1 相同。
为什么是 Rθ−1 ?
上面我们提到逆变换 Inverse Transform,不难看出,在 z-x 平面逆时针旋转 θ 的角度,相当于在 x-z 平面顺时针旋转 θ 的角度,也就是逆时针旋转 -θ 的角度,自然是一个逆变换。
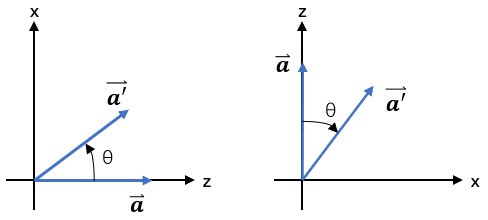
Rθ=[cosθsinθ−sinθcosθ] R−θ=[cos(−θ)sin(−θ)−sin(−θ)cos(−θ)]=[cosθ−sinθsinθcosθ]=RθT R−θ=Rθ−1(bydefinition) 可以得到,旋转矩阵的逆等于旋转矩阵的转置,Rθ−1=RθT,这在后面会用到。
另外在数学上,如果一个矩阵的逆等于它的转置,我们称之为正交矩阵。
3D Rotations
从 Rx、Ry、Rz 组成任何 3D 旋转:
Rxyz(α,β,γ)=Rx(α)Ry(β)Rz(γ) 也就是把任意旋转都写成绕 x,绕 y,绕 z 轴旋转的组合,旋转的角度分别是 α,β,γ 角,这三个角又被称作欧拉角。
三个轴可以对应飞机的运动:横滚 roll、俯仰 pitch、偏航 yaw,可以看出确实任意旋转都可以分解为绕三个轴旋转的组合。
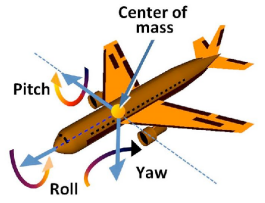
绕 n 轴(用单位向量 n表示,起点为原点,方向是 n 轴的方向),旋转角度 α 的旋转矩阵:
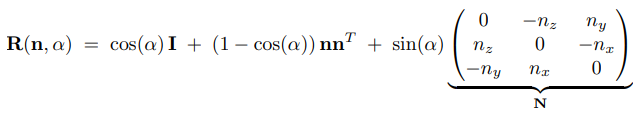
如何绕任意轴旋转?变换分解:将轴起点平移到原点;旋转;再移回去。
但是 R(n,α)+R(n,β)=R(n,2α+β),因为三角函数并不是线性的,也就是说旋转矩阵不适合作差值,四元数可以解决这个问题。
GAMES101没有讲关于四元数,这里先不写了,以后再找一下欧拉角、旋转矩阵、四元数之间的转换。
留个问题,旋转矩阵转欧拉角作差值可以吗?
推导
参考百度百科的过程简单梳理一下:
设 v⇀ 是一个三维空间向量,k是旋转轴的单位向量,则 v⇀ 在右手螺旋定则意义下绕旋转轴 k旋转角度 θ 得到的向量可以由三个不共面的向量 v⇀ , k和 k×v⇀ 表示:
vrot⇀=cosθv⇀+(1−cosθ)(v⇀⋅k)k+sinθk×v⇀ 向量形式
思路:对于与旋转轴 k呈任意角度的向量 v⇀,可以通过正交分解,把被旋转向量转化为与旋转轴平行的分量 v∥⇀ 和与旋转轴垂直的分量 v⊥⇀,其中 v∥⇀ 在旋转中是不变的,而 v⊥⇀ 则恰好旋转了角度 θ,把 v⊥⇀ 旋转后的向量 v⊥rot⇀ 与 v∥⇀ 相加,即可得到旋转以后的向量 vrot⇀=v∥⇀+v⊥rot⇀ 。
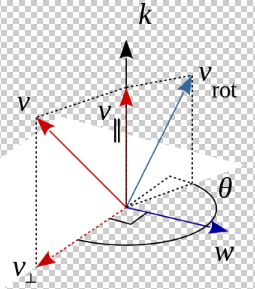
Step 1:
对向量 v⇀ 正交分解:v⇀=v∥⇀+v⊥⇀
利用向量投影公式,可得 v∥⇀,其中设 k与 v⇀ 夹角为 α,且 k为单位向量,∣∣∣k∣∣∣=1
v∥⇀=proj(v⇀,k)=(∣∣∣v⇀∣∣∣cosα)k=(∣∣∣k∣∣∣v⇀⋅k)k=(v⇀⋅k)k 通过向量减法,可得 v⊥⇀=v⇀−v∥⇀=v⇀−(v⇀⋅k)k
Step 2:
首先得到 v⊥⇀ 对应的单位向量 v⊥=normalize(v⊥⇀)=∣v⊥⇀∣v⊥⇀
利用叉乘得到与 k和 v⊥ 都垂直的单位向量 w:
w=k×v⊥=∣∣∣v⊥⇀∣∣∣k×v⊥⇀=∣∣∣v⊥⇀∣∣∣k×(v⇀−(v⇀⋅k)k)=∣∣∣v⊥⇀∣∣∣k×v⇀−0⇀=∣∣∣v⊥⇀∣∣∣k×v⇀ 此时 k,v⊥,w组成一个右手坐标系。
为什么令 w=k×v⊥ 而不是 w=v⊥×k?
个人理解是方便计算:
因为逆时针旋转,一般假设旋转角度 θ(0≤θ≤180∘),正交分解时计算方便,否则要处理负号;后面由 vrot⇀ 推导旋转矩阵时也容易提取 v⇀
当然令 w=v⊥×k也完全 OK,只是某些部分会多一个负号,这只是我们推导的中间过程,最终结果是一样的,因为有 a⇀×b⇀=−b⇀×a⇀
Step 3:
然后可以对旋转 θ 角度之后的 v⊥rot⇀ 作正交分解:
v⊥rot⇀=(∣∣∣v⊥rot⇀∣∣∣cosθ)v⊥+(∣∣∣v⊥rot⇀∣∣∣sinθ)w 显然,有 ∣∣∣v⊥rot⇀∣∣∣=∣∣∣v⊥⇀∣∣∣,所以:
v⊥rot⇀=cosθv⊥⇀+sinθk×v⇀=cosθ(v⇀−(v⇀⋅k)k)+sinθk×v⇀ 最终得到旋转后的向量表达式 vrot⇀:
vrot⇀=v∥⇀+v⊥rot⇀=(v⇀⋅k)k+cosθ(v⇀−(v⇀⋅k)k)+sinθk×v⇀ 即为:
vrot⇀=cosθv⇀+(1−cosθ)(v⇀⋅k)k+sinθk×v⇀ 矩阵形式
在计算机图形学中,罗德里格向量旋转公式通常被用来填写旋转矩阵 R(k,θ)。
旋转以后的向量可以表示为:vrot⇀=R(k,θ)v⇀
只需从向量表达式中提取出一个右乘(点乘)的 v⇀,即可得:
R(k,θ)=cosθI+(1−cosθ)kkT+sinθK 其中,I 为 3 阶单位矩阵(也有用 E 表示的),K 为单位向量 k的矩阵表示:k×v⇀=Kv⇀
假设:k=(kxkykz)T,v⇀=(vxvyvz)T,则:
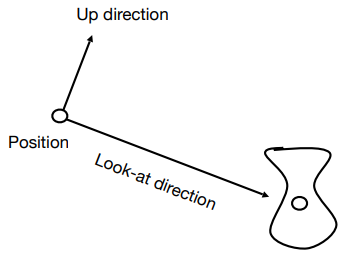
R(k,θ)=cosθI+(1−cosθ)⎝⎛kxkykz⎠⎞(kxkykz)+sinθ⎝⎛0kz−ky−kz0kxky−kx0⎠⎞ - 什么是视图变换?思考如何拍一张照片:
- 找一个好的地方安排人站位(模型变换 Model Transformation)
- 找一个好的角度安置相机(视图变换 View Transformation)
- 茄子!(投影变换 Projection Transformation)
- 如何进行视图变换?
为什么要考虑逆旋转?如果直接计算 Rview:
Rotate g to -Z, tto Y, g×tto X
设旋转矩阵 Rview:
Rview=⎣⎢⎢⎡adg0beh0cfi00001⎦⎥⎥⎤ X,Y,Z 方向分别用单位向量 x,y,z表示:
x=⎝⎜⎜⎛1000⎠⎟⎟⎞y=⎝⎜⎜⎛0100⎠⎟⎟⎞z=⎝⎜⎜⎛0010⎠⎟⎟⎞ 设 g,t,g×t分别为:
g=⎝⎜⎜⎛xgygzg0⎠⎟⎟⎞t=⎝⎜⎜⎛xtytzt0⎠⎟⎟⎞g×t=⎝⎜⎜⎛xg×tyg×tzg×t0⎠⎟⎟⎞ 则有:−z=Rviewg,y=Rviewt,x=Rviewg×t,但是这样计算 Rview 确实有点困难。
考虑它的逆旋转 Inverse rotation:X to g×t, Y to t, Z to −g
设旋转矩阵 Rview−1:
Rview−1=⎣⎢⎢⎡adg0beh0cfi00001⎦⎥⎥⎤ 则有:g×t=Rview−1x,t=Rview−1y,−g=Rview−1z,可以很容易计算出:
Rview−1=⎣⎢⎢⎡xg×tyg×tzg×t0xtytzt0x−gy−gz−g00001⎦⎥⎥⎤ 前面我们提到,正交矩阵的逆等于它的转置,所以 Rview=(Rview−1)−1=(Rview−1)T
Rview=⎣⎢⎢⎡xg×txtx−g0yg×tyty−g0zg×tztz−g00001⎦⎥⎥⎤
- 总结 Summary
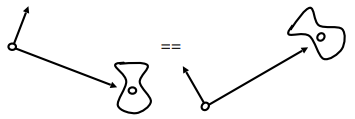
- Transform objects together with the camera
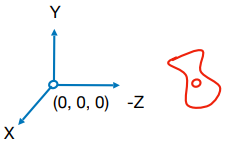
- Until camera at the origin, up at Y, look at -Z
- 视图/相机变换 View/Camera Transformation,也称为模型视图变换 ModelView Transformation
- 我们需要它用于投影变换 Projection Transformation。
这样只需要对物体应用视图变换,相机就固定在默认位置上(The origin, up at Y, look at -Z)。从世界坐标系转到相机坐标系?
- 计算机图形学中的投影
- 3D to 2D
- 正交投影 Orthographic projection
- 透视投影 Perspective projection(近大远小
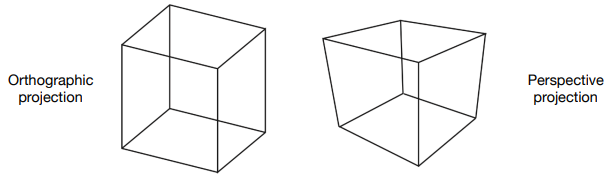
- 正交投影与透视投影的对比
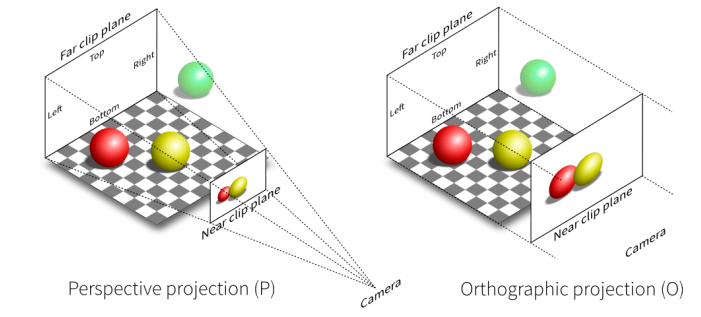
正交投影 Orthographic projection
- 一种简单的理解方式
- 相机位于原点,看向 -Z,向上方向 Y(视图变换中的默认相机位置
- 去掉 Z 轴(映射到 z = 0 的 x-y 平面,3D to 2D
- 将生成的矩形画面平移并缩放到 [−1,1]2
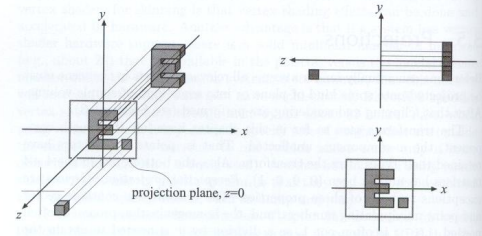
- 通常情况下(规定/默认操作,方便后续计算
- 我们想要将长方体 [l, r] x [b, t] x [f, n] 映射到特定的 “canonical(正则、规范、标准)” 立方体 [−1,1]3
[left, right] → [-1, 1]; [bottom, top] → [-1, 1]; [far, near] → [-1, 1]
- 以简单的方式:
- 移动 translate 长方体的中心 center 到原点 origin
- 缩放 scale 到 “规范 canonical” 立方体
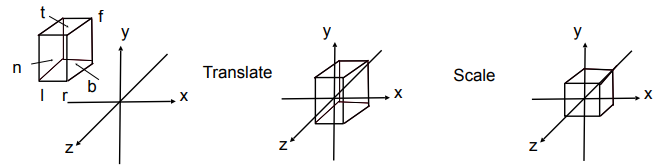
- 变换矩阵
- Translate (center to origin) first, then scale (length/width/height to 2)
Mortho=⎣⎢⎢⎡r−l20000t−b20000n−f200001⎦⎥⎥⎤⎣⎢⎢⎡100001000010−2r+l−2t+b−2n+f1⎦⎥⎥⎤ - 注意事项
- 看向 -Z 方向会使近处 near 和远处 far 反直觉/不直观(n > f)
从坐标来说,直觉应该是近处坐标小,远处坐标大,而这里是 “近大远小”
- 仅供参考:这就是 OpenGL(图形 API)使用左手坐标的原因
将长方体映射到规范立方体,不是等比例压缩,很可能造成拉伸,这没关系,后面还有变换处理。
透视投影 Perspective projection
- 最常见于计算机图形学、艺术、视觉系统
- 更远的物体更小(近大远小
- 视觉效果:平行线不平行,收敛到单点
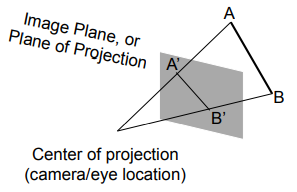
- 如何进行透视投影?
- 首先将四角棱台/锥台 frustum (视锥体 viewing frustum) “挤压” 变成长方体 cuboid
这样就将透视投影转换成正交投影 Mpersp−>ortho - 然后进行正交投影(我们前面已经准备好 Mortho
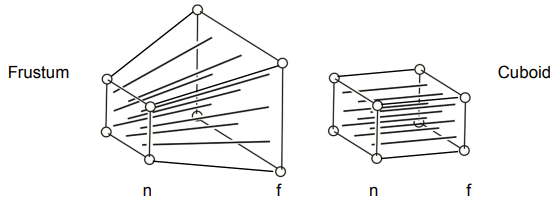
这里我们规定 “挤压” 操作以确保做法唯一:
- 近平面 (z = n) 上的任意点都不会改变
- 远平面 (z = f) 上的任意点的 z 坐标不会改变
- 远平面 (z = f) 上的中心点也不会改变
(frustum 内部的点坐标会发生变化,包括 z 坐标
- 如何 “挤压” ?寻找一种变换 transformation
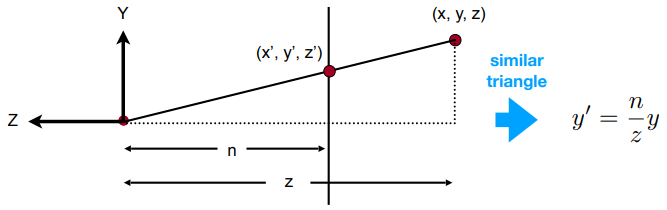
- 寻找变换后的点 (x′,y′,z′) 和原始点 (x,y,z) 之间的关系(相似三角形
由相似三角形的成比例关系,可以得到 frustum 中任意点的 x, y 坐标的变换:x′=nx/z,y′=ny/z
但是 z 坐标的变换仍是未知的,暂且写为 unknown
- 在齐次坐标 homogeneous coordinates 中:
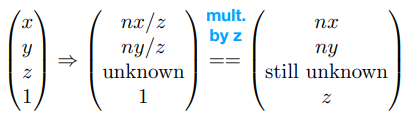
回想之前讲过的齐次坐标的性质:
(wx,wy,wz,w),w=0 和 (x,y,z,1) 表示的是 3D 中的同一点 (x,y,z)
例如:(1, 0, 0, 1) 和 (2, 0, 0, 2) 都表示 (1, 0, 0)
所以我们可以同时乘上一个 z (mult. by z):(x,y,z,1) to (xz,yz,zz,z)
Mpersp→ortho(4×4)⎝⎜⎜⎛xyz1⎠⎟⎟⎞=⎝⎜⎜⎛nx/zny/zunknown1⎠⎟⎟⎞=⎝⎜⎜⎛nxnyunknownz⎠⎟⎟⎞ - 根据已知信息,已经足以弄清楚 Mpersp−>ortho 的一部分:
Mpersp→ortho=⎝⎜⎜⎛n0?00n?000?100?0⎠⎟⎟⎞ - 显然,变换矩阵的第三行负责的是 z 坐标
近平面 (z = n) 上的任意点都不会改变:(x, y, n, 1) to (x, y, n, 1)

所以第三行一定是 (00AB) 的形式
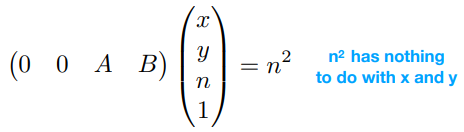
同时,已知:An+B=n2
远平面 (z = f) 上的任意点的 z 坐标不会改变:(x,y,f,1) to (x′,y′,f,1)
取远平面的中心点:(0,0,f,1) to (0,0,f,1)
可得 Af+B=f2
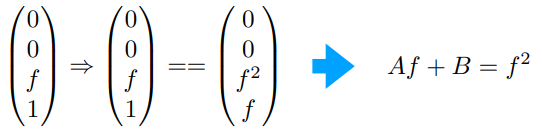
求解 A 和 B:

- 最终,得到 Mpersp→ortho:
Mpersp→ortho=⎝⎜⎜⎛n0000n0000n+f100−nf0⎠⎟⎟⎞ - 接下来?
- 进行正交投影 Mortho
- Mpersp=MorthoMpersp→ortho
Mpersp→ortho=⎣⎢⎢⎡r−l20000t−b20000n−f200001⎦⎥⎥⎤⎣⎢⎢⎡100001000010−2r+l−2t+b−2n+f1⎦⎥⎥⎤⎝⎜⎜⎛n0000n0000n+f100−nf0⎠⎟⎟⎞ 最后的小问题:frustum 中间平面 z=2n+f 的点,经过 “挤压” 后会变得更远还是更近?
我们只关注 z 坐标的变化,可以观察中间平面的中心点 (002n+f1)
记该点为 V 点,坐标系原点为 O 点,v⇀=OV⇀
则有:v⇀persp→ortho=Mpersp→orthov⇀
v⇀persp→ortho=⎝⎜⎜⎛n0000n0000n+f100−nf0⎠⎟⎟⎞⎝⎜⎜⎛002n+f1⎠⎟⎟⎞=⎝⎜⎜⎛00n+f−n+f2nf1⎠⎟⎟⎞ 比较 zpersp→ortho=n+f−n+f2nf 和 z=2n+f 的大小:
假设 △=zpersp→ortho−z
△=2n+f−n+f2nf=2(n+f)(n+f)2−4nf=2(n+f)(n−f)2 因为相机位置在原点,看向 -Z,应该有:f < n < 0,则 △<0
也就是 zpersp→ortho<z,所以是变远了
事实上,对远近平面中间的任意点,可以类似以上证明得出结论:“挤压” 后都会变远。
[GAMES101] 投影变换和模型变换