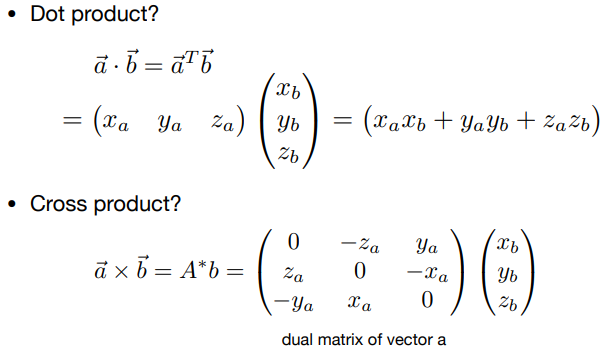Review of Linear Algebra
向量:Vectors
通常写作 或
或使用起点和终点
表示方向和长度
没有绝对的起点位置(不关心绝对位置,可以平移移动
向量规范化:Vector Normalization
向量的长度写作
单位向量
一个长度为 1 的向量
一个向量的单位向量:
用来表示方向(不关心长度)
向量加法:Vector Addition
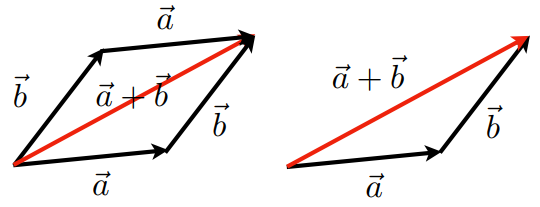
几何上:平行四边形法则、三角形法则(不止适用于两个向量)
代数上:坐标相加
笛卡尔坐标系(直角坐标系):Cartesian Coordinates
向量的坐标表示,默认列向量,计算长度。

向量乘法:Vector Multiplication
点乘(标量):Dot (scalar) Product
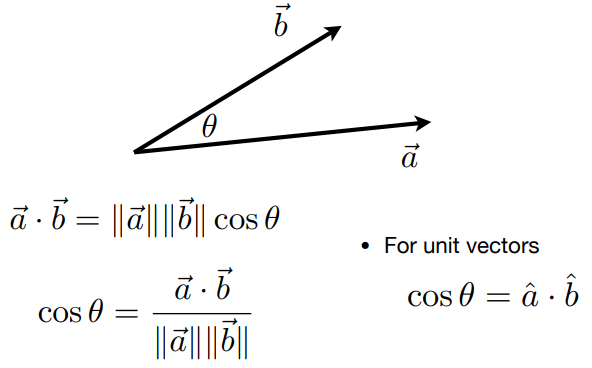
向量点乘的结果是标量(一个数)。
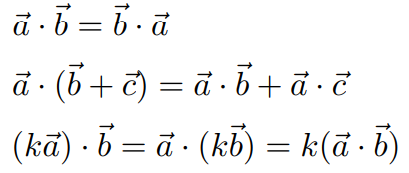
笛卡尔坐标系中的点乘:对应元素相乘,然后相加(可以扩展到高维)。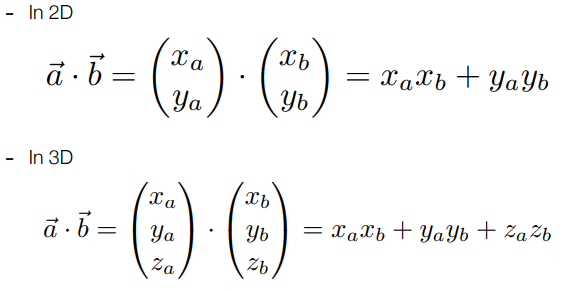
点乘的作用(图形学中):
找到两个向量(方向)之间的夹角,比如光源和表面之间夹角的余弦值
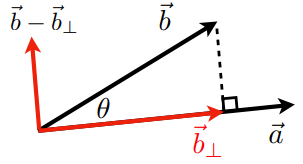
找到一个向量在另一个向量上的投影
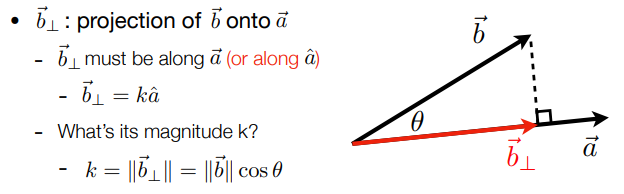
分解向量(垂直与平行的分解)
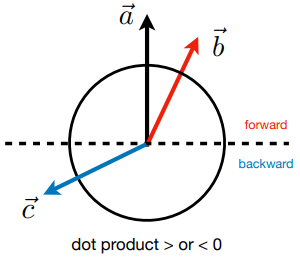
测量两个向量方向的接近程度(-1 ~ 1,-1 完全相反,1 完全同向)
得到两个向量的方向性( >0 基本一致,<0 基本相反,=0 垂直)
叉乘(矢量):Cross (vector) Product
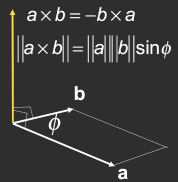
叉乘结果与两个初始向量正交(垂直)
方向由右手定则确定(叉乘不满足交换律)
在构建坐标系时有用
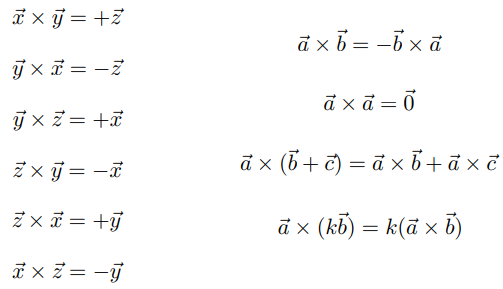
在三维坐标系中,如果有 ,即为右手坐标系。
叉乘的笛卡尔公式: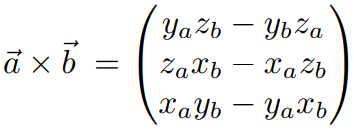
向量的叉乘可以表示为矩阵形式: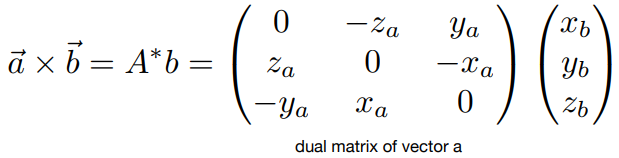
叉乘的作用(图形学中):
判定一个点或一个向量,在另一个向量方向的 左 / 右
,在 的右侧,在 的左侧判定一个点在三角形(可扩展多边形)的 内 / 外
下图 中,,,的结果向量方向都是向外的(同向),说明点 P 均在 ,,的左侧,说明点 P 在 内。简言之,三角形的三条边所代表的三个向量(顺时针或逆时针),与三个点与点 P 构成的向量的叉乘的结果,三个结果向量都是同向的,说明点 P 在三条边的同侧,则点 P 在三角形中。
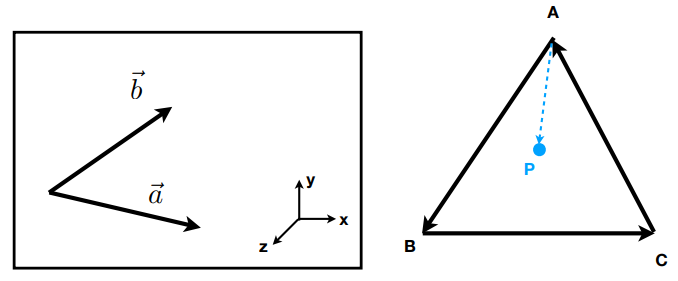
如果叉乘结果等于 0,说明计算的两个向量重合,自己决定在左或右,内或外,都行。
正交基和坐标系:Orthonormal bases and coordinate frames
对于表示点、位置、地点(points, positions, locations)很重要
通常,多组坐标系:全局坐标系、局部坐标系、世界坐标系、模型、模型的各个部分(头、手…)
关键问题是这些系统(坐标系)之间的转换
任意一个三维向量可以表示在一个三维的直角坐标系中:

利用点乘分解向量(投影),可以用单位向量 ,,表示任意三维向量 :
矩阵:Matrices
在图形学中,普遍用于表示变换 - 平移、旋转、剪切、缩放(Translation, rotation, shear, scale)
矩阵加法、矩阵乘法(略)
M行N列矩阵 乘 N行P列矩阵 结果为 M行P列矩阵:(M x N)(N x P) = (M x P)
矩阵乘法不满足交换律,AB 和 BA 一般是不同的。
- (AB)C = A(BC)
- A(B + C) = AB + AC
- (A + B)C = AC + BC
矩阵转置,
单位矩阵 ,
矩阵的逆:,
向量乘法的矩阵形式: