写一个函数,输入 n ,求斐波那契(Fibonacci)数列的第 n 项(即 F(N))。斐波那契数列的定义如下:F(0) = 0, F(1) = 1, F(N) = F(N - 1) + F(N - 2), 其中 N > 1。To do it! 示例1 输入: n = 2,输出: 1示例2 输入: n = 5,输出: 5提示: 0 <= n <= 100
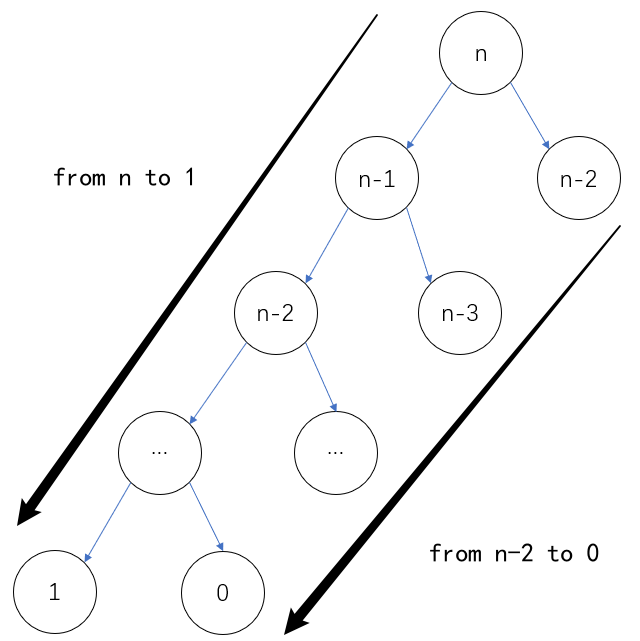
采用暴力递归的方式包含了大量重复的递归计算,例如 f(n - 1) 和 f(n - 2) 两者向下递归需要各自计算 f(n - 2) ,总时间复杂度为 O(2 n 2^n 2 n ,时间超限。我们可以新建一个长度为 n + 1 的数组,用于递归时存储 f(0) 到 f(n) 的值,重复遇到某个数字就直接从数组中取用,避免了重复的递归计算。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 class Solution { unordered_map<int , int > f; const int mod = 1000000007 ; public : int fib (int n) if (n < 2 ) return n; if (f.find (n) != f.end ()) return f[n]; f[n] = (fib (n - 1 ) + fib (n - 2 )) % mod; return f[n]; } }; class Solution {private : const int mod = 1000000007 ; vector<int > arr; int f (int n) if (n < 2 ) return n; if (arr[n] != -1 ) return arr[n]; arr[n] = (f (n - 1 ) + f (n - 2 )) % MOD; return arr[n]; } public : int fib (int n) arr = vector <int >(n + 1 , -1 ); return f (n); } };
每个数值只计算一次,再遇到就不往下计算了,所以节点数即递归次数,为 2n - 1 次。O(1) ,递归次数为 O(2n - 1) = O(n) 。还有额外空间为 O(n) 的数组。时间复杂度:O(n) ,空间复杂度:O(n)
递归是自上而下的求解过程,我们可以自下而上,求 f(0), f(1), f(2) = f(1) + f(0), f(3) = f(2) + (1) ,此时 f(0) 的值已经用不到了,利用 f(n) = f(n - 1) + f(n - 2) ,每次计算只需要存储三个值。a, b, c:
a = f(0), b = f(1), c = a + b = f(2)a = b = f(1), b = c = f(2), c = a + b = f(3)a = b = f(2), b = c = f(3), c = a + b = f(4)… 斐波那契数存在递归关系,即可用动态规划求解。动态规划的转移方程即为递推关系方程,边界条件就是 f(0), f(1) 。本应该利用长度为 n 的数组以循环实现,但是我们只需要存储三个值,便可把空间复杂度优化为 O(1) 。算法详解
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution {private : const int MOD = 1000000007 ; public : int fib (int n) if (n <= 1 ) return n; int a = 0 , b = 1 , c = a + b; for (int i = 3 ; i <= n; i++) { a = b; b = c; c = (a + b) % MOD; } return c; } };
时间复杂度:O(n) ,空间复杂度:O(1)
使用矩阵快速幂的方法可以降低时间复杂度。首先我们构建这样一个递推关系:
[ 1 1 1 0 ] [ F ( n ) F ( n − 1 ) ] = [ F ( n ) + F ( n − 1 ) F ( n ) ] = [ F ( n + 1 ) F ( n ) ] \begin{bmatrix}1&1\\1&0\end{bmatrix}\begin{bmatrix}F(n)\\F(n-1)\end{bmatrix}\;=\;\begin{bmatrix}F(n)\;+\;F(n-1)\\F(n)\end{bmatrix}\;=\;\begin{bmatrix}F(n+1)\\F(n)\end{bmatrix} [ 1 1 1 0 ] [ F ( n ) F ( n − 1 ) ] = [ F ( n ) + F ( n − 1 ) F ( n ) ] = [ F ( n + 1 ) F ( n ) ]
于是:
[ F ( n + 1 ) F ( n ) ] = [ 1 1 1 0 ] n [ F ( 1 ) F ( 0 ) ] \begin{bmatrix}F(n+1)\\F(n)\end{bmatrix}\;=\;\;\begin{bmatrix}1&1\\1&0\end{bmatrix}^n\begin{bmatrix}F(1)\\F(0)\end{bmatrix} [ F ( n + 1 ) F ( n ) ] = [ 1 1 1 0 ] n [ F ( 1 ) F ( 0 ) ]
令:
M = [ 1 1 1 0 ] M\;=\;\begin{bmatrix}1&1\\1&0\end{bmatrix} M = [ 1 1 1 0 ]
所以我们只需快速计算矩阵 M 的 n 次幂,就可以得到 F(n) 的值。如果直接求取 M n M^n M n O(n) ,可以定义矩阵乘法,然后用快速幂算法来加速这里 M n M^n M n 快速幂 & 矩阵快速幂 笔记
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 class Solution { const int mod = 1000000007 ; vector<vector<long >> multiply (vector<vector<long >>& a, vector<vector<long >>& b) { vector<vector<long >> ret (2 , vector <long >(2 , 0 )); for (int i = 0 ; i < 2 ; ++i) { for (int j = 0 ; j < 2 ; ++j) { for (int k = 0 ; k < 2 ; ++k) { ret[i][j] += a[i][k] * b[k][j]; } ret[i][j] %= mod; } } return ret; } vector<vector<long >> pow (vector<vector<long >>& M, int n) { vector<vector<long >> ret = {{1 , 0 }, {0 , 1 }}; while (n > 0 ) { if (n & 1 ) ret = multiply (ret, M); n >>= 1 ; M = multiply (M, M); } return ret; } public : int fib (int n) if (n < 2 ) return n; vector<vector<long >> M = {{1 , 1 }, {1 , 0 }}; return pow (M, n - 1 )[0 ][0 ]; } };
multiply时间复杂度为 O(1) ,pow时间复杂度为 O(log 2 n \log_2n log 2 n ,即 n 的二进制位数,所以总时间复杂度为 O(log n) 。时间复杂度:O(log n) ,空间复杂度:O(1)